회귀 (Regression) 예측

0. 데이터 셋
- 0-1. 데이터 로드
- 0-2. 데이터프레임 만들기
1. Training set / Test set 나누기
2. 평가 지표 만들기
3. 회귀 알고리즘
- 3-1. Linear Regression
- 3-2. Ridge & LASSO & ElasticNet
  - (1) 개념
  - (2) 실습
4. Scaling
- 4-1. Scaler 소개
- 4-2. Scaling 후 모델 학습 – 파이프라인 활용
5. Polynomial Features

[Supervised Learning] Document

특성: 수치형 값을 예측 (Y의 값이 연속형 수치로 표현)

예시:

주택 가격 예측
매출앵 예측

0. 데이터 셋

import pandas as pd
import numpy as np

np.set_printoptions(suppress=True) # If True, print floating point numbers instead of scientific notation

1	from sklearn.datasets import load_boston

[Boston Dataset]

0-1. 데이터 로드

1	data = load_boston()

1	print(data['DESCR']) # data description

.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
.. topic:: References

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

0-2. 데이터프레임 만들기

# step 1. features (X)
# data['data'] - feature data; data['feature_names'] - feature column names

df = pd.DataFrame(data['data'], columns = data['feature_names'])

# step 2. target (y) 추가 
df['MEDV'] = data['target']

df.head()

	CRIM	ZN	INDUS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	396.90	5.33	36.2

컬럼 소게 (feature 13 + target 1):

CRIM: 범죄율
ZN: 25,000 square feet 당 주거용 토지의 비율
INDUS: 비소매(non-retail) 비즈니스 면적 비율
CHAS: 찰스 강 더미 변수 (통로가 하천을 향하면 1; 그렇지 않으면 0)
NOX: 산화 질소 농도 (천만 분의 1)
RM:주거 당 평균 객실 수
AGE: 1940 년 이전에 건축된 자가 소유 점유 비율
DIS: 5 개의 보스턴 고용 센터까지의 가중 거리
RAD: 고속도로 접근성 지수
TAX: 10,000 달러 당 전체 가치 재산 세율
PTRATIO 도시 별 학생-교사 비율
B: 1000 (Bk-0.63) ^ 2 여기서 Bk는 도시 별 검정 비율입니다.
LSTAT: 인구의 낮은 지위
MEDV: 자가 주택의 중앙값 (1,000 달러 단위)

1. Training set / Test set 나누기

1	from sklearn.model_selection import train_test_split

1	x_train, x_test, y_train, y_test = train_test_split(df.drop('MEDV', 1), df['MEDV'], random_state=23)

1	x_train.shape, y_train.shape

((379, 13), (379,))

1	x_test.shape, y_test.shape

((127, 13), (127,))

1	x_train.head()

	CRIM	ZN	INDUS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
112	0.12329	0.0	10.01	0.547	5.913	92.9	2.3534	6.0	432.0	17.8	394.95	16.21
301	0.03537	34.0	6.09	0.433	6.590	40.4	5.4917	7.0	329.0	16.1	395.75	9.50
401	14.23620	0.0	18.10	0.693	6.343	100.0	1.5741	24.0	666.0	20.2	396.90	20.32
177	0.05425	0.0	4.05	0.510	6.315	73.4	3.3175	5.0	296.0	16.6	395.60	6.29
69	0.12816	12.5	6.07	0.409	5.885	33.0	6.4980	4.0	345.0	18.9	396.90	8.79

1	y_train.head()

112    18.8
301    22.0
401     7.2
177    24.6
69     20.9
Name: MEDV, dtype: float64

2. 평가 지표 만들기

2-1. 평가 지표 계산식

(1) MAE (Mean Absolute Error)

MAE (평균 절대 오차): 에측값과 실제값의 차이의 절대값에 대하여 평균을 낸 것

MAE = \frac{1}{n} \sum_{i=1}^n \left\vert y_i - \widehat{y_i} \right\vert

(2) MSE (Mean Squared Error)

MSE (평균 제곱 오차): 예측값과 실제값의 차이의 제곱에 대하여 평균을 낸 것

MSE = \frac{1}{n} \sum_{i=1}^n \left( y_i - \widehat{y_i} \right)^2

(3) RMSE (Root Mean Squared Error)

RMSE (평균 제곱근 오차): 예측값과 실제값의 차이의 제곱에 대하여 평균을 낸 뒤 루트를 씌운 것

RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^n \left( y_i - \widehat{y_i} \right)^2}

2-2. 코딩으로 평가 지표 만들어 보기

1	import numpy as np

1 2	actual = np.array([1, 2, 3]) pred = np.array([3, 4, 5])

# MAE
def my_mae(actual, pred):
    return np.abs(actual - pred).mean()

my_mae(actual, pred)

2.0

# MSE
def my_mse(actual, pred):
    return ((actual - pred)**2).mean()

my_mse(actual, pred)

4.0

# RMSE
def my_rmse(actual, pred):
    return np.sqrt(my_mse(actual, pred))

my_rmse(actual, pred)

2.0

2-3. sklearn의 평가 지표 활용하기

1	from sklearn.metrics import mean_absolute_error, mean_squared_error

[sklearn.metrics.mean_absolute_error]
[sklearn.metrics.mean_squared_error]

1 2	# MAE (my_mae VS sklearn_mae) my_mae(actual, pred), mean_absolute_error(actual, pred)

(2.0, 2.0)

1 2	# MSE (my_mse VS sklearn_mse) my_mse(actual, pred), mean_squared_error(actual, pred)

(4.0, 4.0)

2-4. 모델 성능 확인을 위한 함수

import matplotlib.pyplot as plt
import seaborn as sns

my_predictions = {}

colors = ['r', 'c', 'm', 'y', 'k', 'khaki', 'teal', 'orchid', 'sandybrown',
          'greenyellow', 'dodgerblue', 'deepskyblue', 'rosybrown', 'firebrick',
          'deeppink', 'crimson', 'salmon', 'darkred', 'olivedrab', 'olive', 
          'forestgreen', 'royalblue', 'indigo', 'navy', 'mediumpurple', 'chocolate',
          'gold', 'darkorange', 'seagreen', 'turquoise', 'steelblue', 'slategray', 
          'peru', 'midnightblue', 'slateblue', 'dimgray', 'cadetblue', 'tomato'
         ]

# prediction plot
def plot_predictions(name_, actual, pred):
    df = pd.DataFrame({'actual': y_test, 'prediction': pred})
    df = df.sort_values(by='actual').reset_index(drop=True)

    plt.figure(figsize=(12, 9))
    plt.scatter(df.index, df['prediction'], marker='x', color='r')
    plt.scatter(df.index, df['actual'], alpha=0.7, marker='o', color='black')
    plt.title(name_, fontsize=15)
    plt.legend(['prediction', 'actual'], fontsize=12)
    plt.show()

# evaluation plot
def mse_eval(name_, actual, pred):
    global predictions
    global colors

    plot_predictions(name_, actual, pred)

    mse = mean_squared_error(actual, pred)
    my_predictions[name_] = mse

    y_value = sorted(my_predictions.items(), key=lambda x: x[1], reverse=True)
    
    df = pd.DataFrame(y_value, columns=['model', 'mse'])
    print(df)
    min_ = df['mse'].min() - 10
    max_ = df['mse'].max() + 10
    
    length = len(df)
    
    plt.figure(figsize=(10, length))
    ax = plt.subplot()
    ax.set_yticks(np.arange(len(df)))
    ax.set_yticklabels(df['model'], fontsize=15)
    bars = ax.barh(np.arange(len(df)), df['mse'])
    
    for i, v in enumerate(df['mse']):
        idx = np.random.choice(len(colors))
        bars[i].set_color(colors[idx])
        ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=15, fontweight='bold')
        
    plt.title('MSE Error', fontsize=18)
    plt.xlim(min_, max_)
    
    plt.show()

# remove model
def remove_model(name_):
    global my_predictions
    try:
        del my_predictions[name_]
    except KeyError:
        return False
    return True

3. 회귀 알고리즘

3-1. Linear Regression

[sklearn.linear_model.LinearRegression] Document

1	from sklearn.linear_model import LinearRegression

1
2
3

model = LinearRegression(n_jobs=-1)  # n_jobs: CPU코어의 사용
model.fit(x_train, y_train)
pred = model.predict(x_test)

1	mse_eval('LinearRegression', y_test, pred)

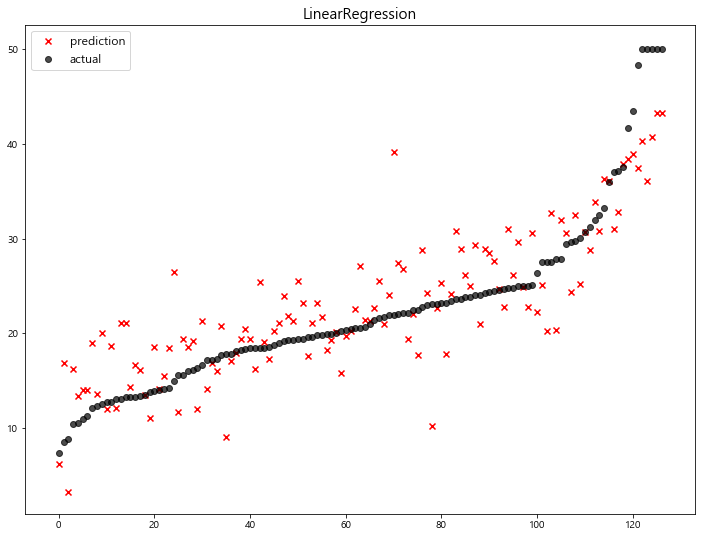
output_59_0

              model        mse
0  LinearRegression  22.770784

output_59_2

3-2. Ridge & LASSO & ElasticNet

(1) 개념

참고

규제(Regularization): 학습이 과적합 되는 것을 방지하고자 일종의 penalty를 부여하는 것.
[원리] penalty를 부여하여 가중치( $\beta$ )를 축소함으로써 학습 모델의 예측 variance를 감소 시키는 것

>> L2 규제 & Ridge (릿지)

L2 규제 (L2 Regularization): 각 가중치 제곱의 합에 규제 강도 (Regularization Strength) $\lambda$ 를 곱한다
$L2 \ 규제 = \lambda \sum_{j=1}^p \beta_j^2 = \lambda\ \lVert \beta \rVert_2^2$ $l_2 \ norm: \lVert \beta \rVert_2 = \sqrt{\sum_{j=1}^p \beta_j^2}$
Ridge: Loss Function에 L2 규제를 더한 값을 최소화 시키는 것
$\min_{\beta_j} \ \left[ \sum_{i=1}^n \left( y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij} \right) + \lambda\ \sum_{j=1}^p\beta_j^2 \right]= \min_{\beta_j} \ \left[ RSS + \lambda\ \sum_{j=1}^p\beta_j^2 \right]$
$\lambda$ 를 크게 하면 가중치( $\beta$ ) 가 더 많이 감소되고(규제를 중요시 함), $\lambda$ 를 작게 하면 가중치( $\beta$ ) 가 증가한다(규제를 중요시하지 않음)

>> L1 규제 & LASSO (라쏘)

L1 규제 (L1 Regularization): 각 가중치 절대값의 합에 규제 강도 (Regularization Strength) $\lambda$ 를 곱한다
$L1\ 규제 = \lambda \sum_{j=1}^p \left| \beta_j \right| = \lambda \ \lVert \beta \rVert_1$ $l1\ norm: \lVert \beta \rVert_1 = \sum_{j=1}^p \left| \beta_j \right|$
LASSO: Loss Function에 L1 규제를 더한 값을 최소화 시키는 것
$\min_{\beta_j} \ \left[ \sum_{i=1}^n \left( y_i-\beta_0-\sum_{j=1}^p\beta_jx_{ij} \right) + \lambda \sum_{j=1}^p \left| \beta_j \right| \right]= \min_{\beta_j} \ \left[ RSS + \lambda \sum_{j=1}^p \left| \beta_j \right| \right]$
어떤 가중치( $\beta$ ) 는 실제로 0이 된다. 즉, 모델에서 완전히 제외되는 특성이 생기는 것이다

>> ElasticNet

l1_ratio (default=0.5)

l1_ratio = 0 (L2 규제만 사용)
l1_ratio = 1 (L1 규제만 사용)
0 < l1_ratio <1 (L1 and L2 규제 혼합사용)

(2) 실습

>> Ridge [Document]

1	from sklearn.linear_model import Ridge

예측 결과 확인

# lambda (규제강도) 범위 설정
alphas = [100, 10, 1, 0.1, 0.01, 0.001]

# 모델 학습
for alpha in alphas:
    ridge = Ridge(alpha = alpha)
    ridge.fit(x_train, y_train)
    ridge_pred = ridge.predict(x_test)
    mse_eval('Ridge(alpha={})'.format(alpha), y_test, ridge_pred)

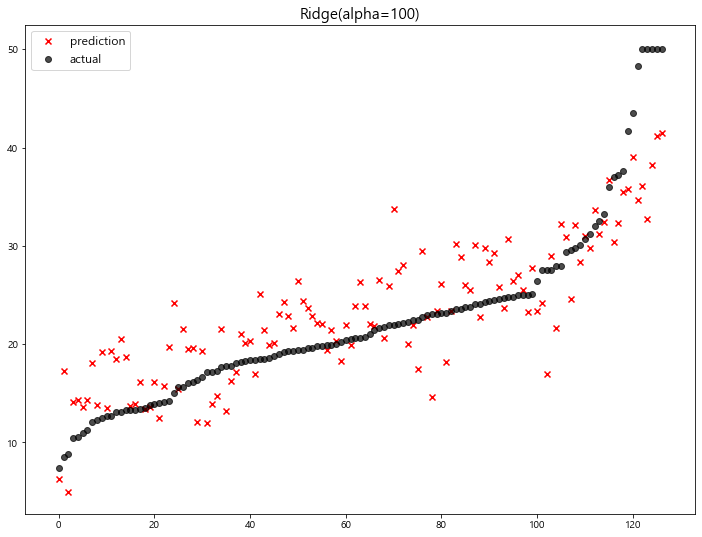
output_75_0

              model        mse
0  Ridge(alpha=100)  23.487453
1  LinearRegression  22.770784

output_75_2

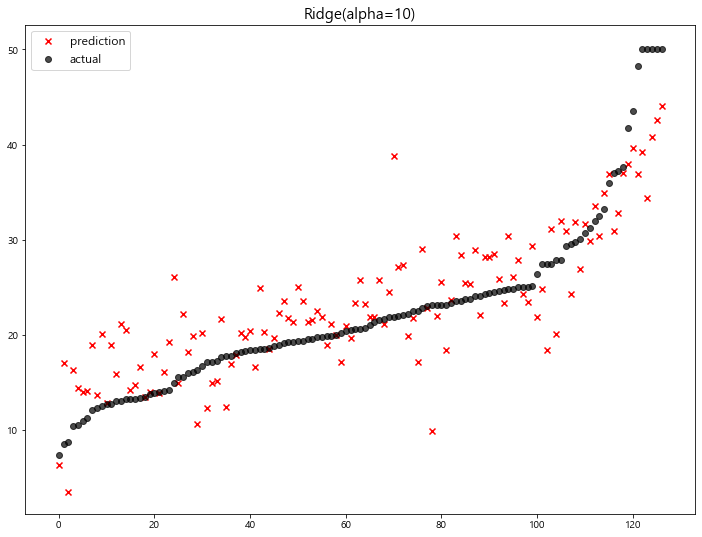
output_75_3

              model        mse
0  Ridge(alpha=100)  23.487453
1   Ridge(alpha=10)  22.793119
2  LinearRegression  22.770784

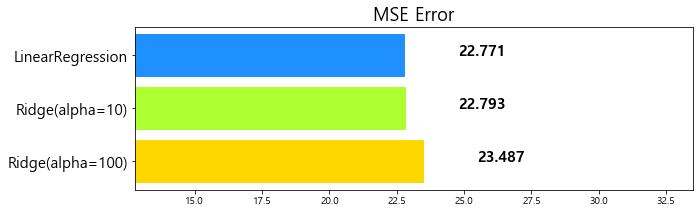
output_75_5

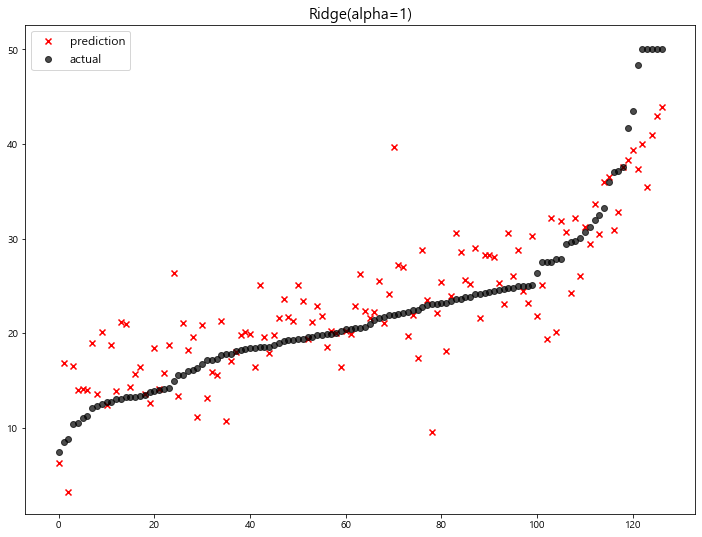
output_75_6

              model        mse
0  Ridge(alpha=100)  23.487453
1   Ridge(alpha=10)  22.793119
2  LinearRegression  22.770784
3    Ridge(alpha=1)  22.690411

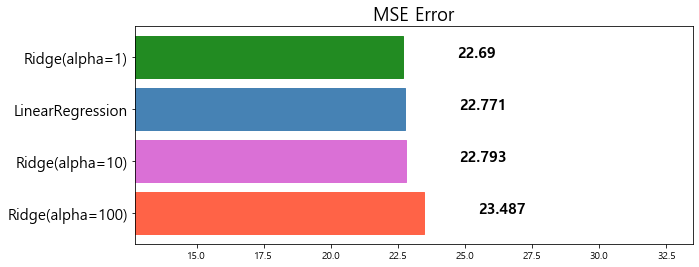
output_75_8

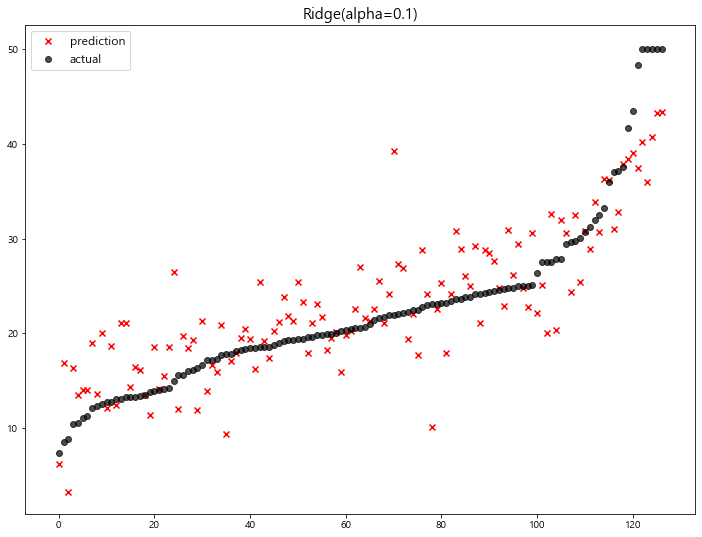
output_75_9

              model        mse
0  Ridge(alpha=100)  23.487453
1   Ridge(alpha=10)  22.793119
2  LinearRegression  22.770784
3  Ridge(alpha=0.1)  22.718126
4    Ridge(alpha=1)  22.690411

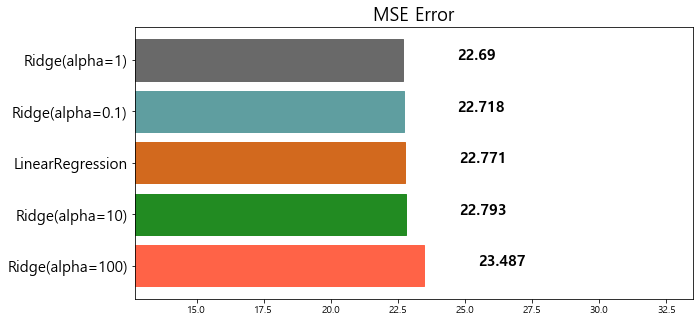
output_75_11

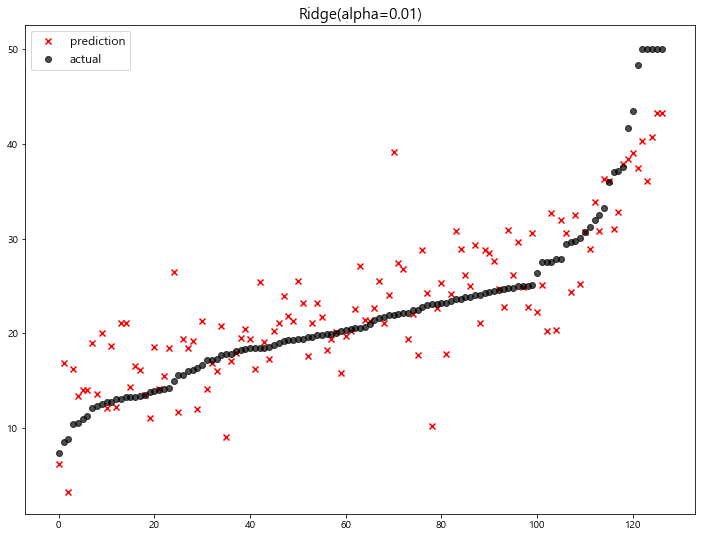
output_75_12

               model        mse
0   Ridge(alpha=100)  23.487453
1    Ridge(alpha=10)  22.793119
2   LinearRegression  22.770784
3  Ridge(alpha=0.01)  22.764254
4   Ridge(alpha=0.1)  22.718126
5     Ridge(alpha=1)  22.690411

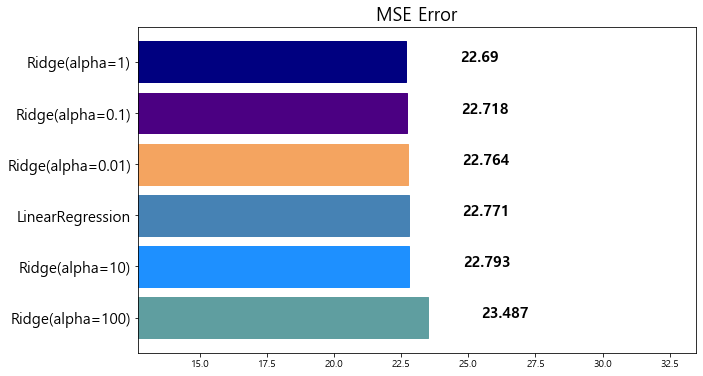
output_75_14

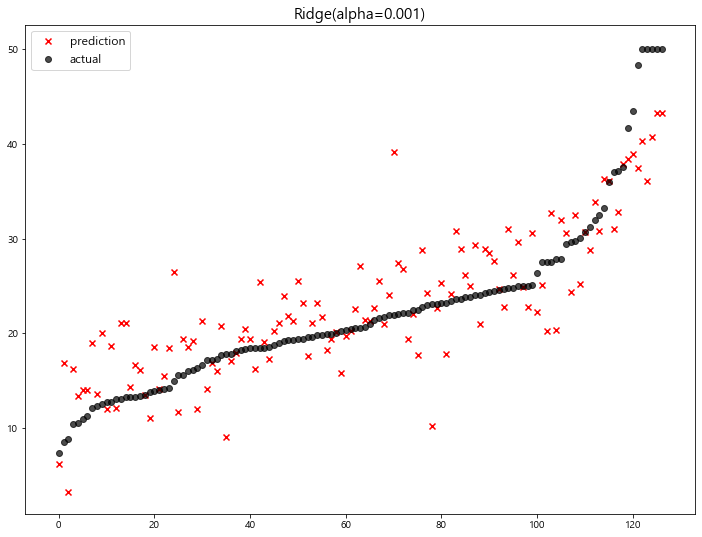
output_75_15

                model        mse
0    Ridge(alpha=100)  23.487453
1     Ridge(alpha=10)  22.793119
2    LinearRegression  22.770784
3  Ridge(alpha=0.001)  22.770117
4   Ridge(alpha=0.01)  22.764254
5    Ridge(alpha=0.1)  22.718126
6      Ridge(alpha=1)  22.690411

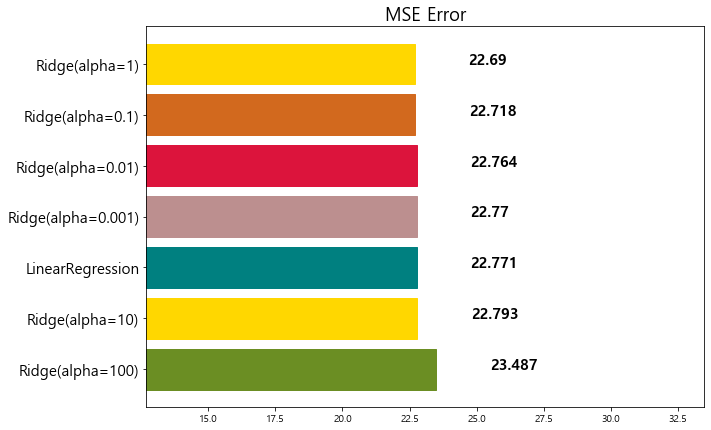
output_75_17

coefficents 값 확인

1	x_train.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
       'PTRATIO', 'B', 'LSTAT'],
      dtype='object')

1	ridge.coef_ # for the last alpha in 'alphas'

array([ -0.09608448,   0.04753482,   0.0259022 ,   3.24479273,
       -18.89579975,   4.06725732,   0.0020486 ,  -1.46883742,
         0.28149275,  -0.0094656 ,  -0.87454099,   0.01240815,
        -0.52406249])

# coefficients visulization

def plot_coef(columns, coef):
    coef_df = pd.DataFrame(list(zip(columns, coef)))
    coef_df.columns=['feature', 'coef']
    coef_df = coef_df.sort_values('coef', ascending=False).reset_index(drop=True)
    
    fig, ax = plt.subplots(figsize=(9, 7))
    ax.barh(np.arange(len(coef_df)), coef_df['coef'])
    idx = np.arange(len(coef_df))
    ax.set_yticks(idx)
    ax.set_yticklabels(coef_df['feature'])
    fig.tight_layout()
    plt.show()

1	plot_coef(x_train.columns, ridge.coef_) # alpha = 0.001

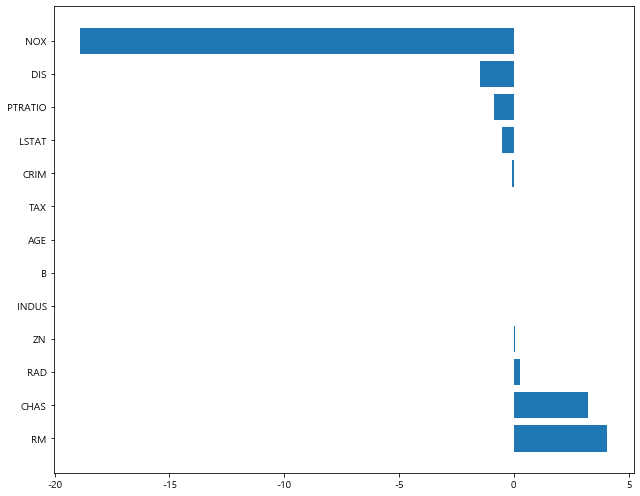
output_81_0

alpha 값에 따른 coef의 차이

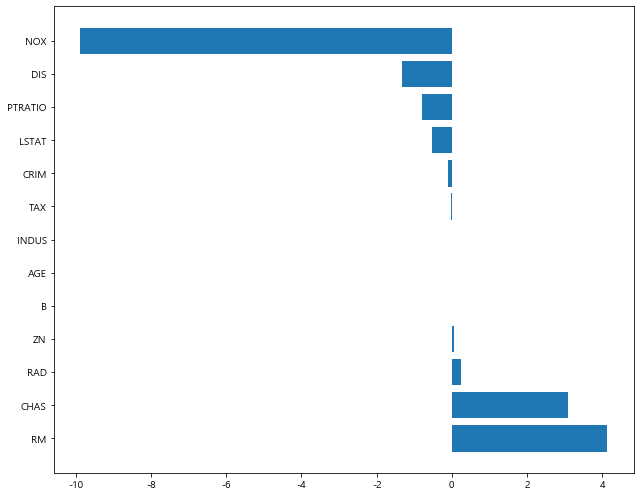
ridge_1 = Ridge(alpha=1)
ridge_1.fit(x_train, y_train)
ridge_pred_1 = ridge_1.predict(x_test)

ridge_100 = Ridge(alpha=100)
ridge_100.fit(x_train, y_train)
ridge_pred_100 = ridge_100.predict(x_test)

1	plot_coef(x_train.columns, ridge_1.coef_) # alpha = 1

output_85_0

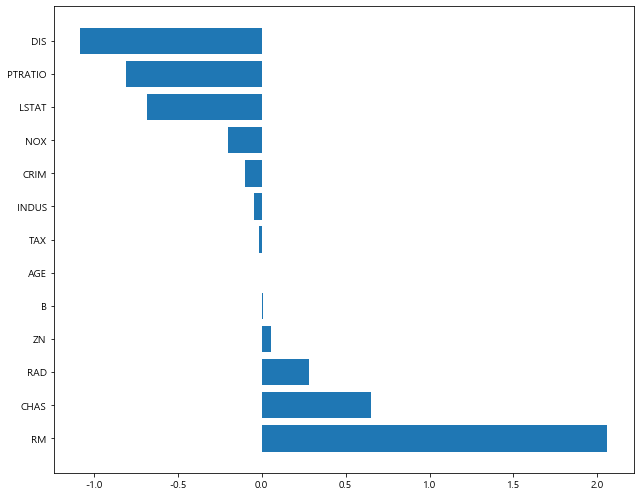
1	plot_coef(x_train.columns, ridge_100.coef_) # alpha = 100

output_86_0

>> LASSO [Document]

1	from sklearn.linear_model import Lasso

예측 결과 확인

# lambda (규제강도) 범위 설정
alphas = [100, 10, 1, 0.1, 0.01, 0.001]

# 모델 학습
for alpha in alphas:
    lasso = Lasso(alpha=alpha)
    lasso.fit(x_train, y_train)
    lasso_pred = lasso.predict(x_test)
    mse_eval('Lasso(alpha={})'.format(alpha), y_test, lasso_pred)

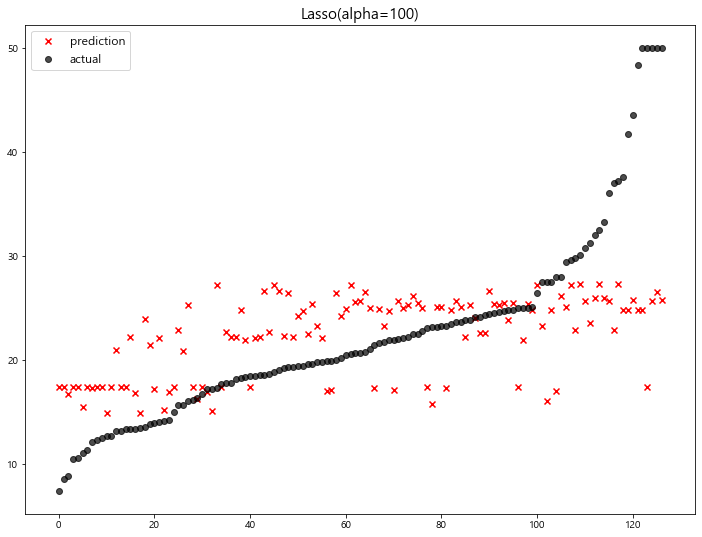
output_92_0

                model        mse
0    Lasso(alpha=100)  63.348818
1    Ridge(alpha=100)  23.487453
2     Ridge(alpha=10)  22.793119
3    LinearRegression  22.770784
4  Ridge(alpha=0.001)  22.770117
5   Ridge(alpha=0.01)  22.764254
6    Ridge(alpha=0.1)  22.718126
7      Ridge(alpha=1)  22.690411

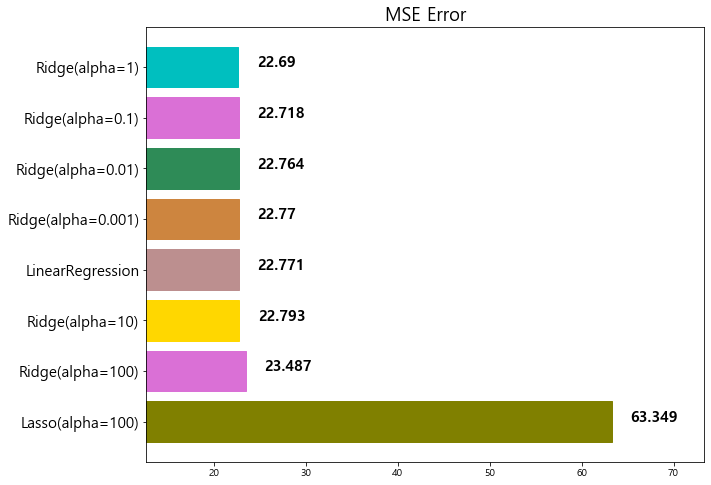
output_92_2

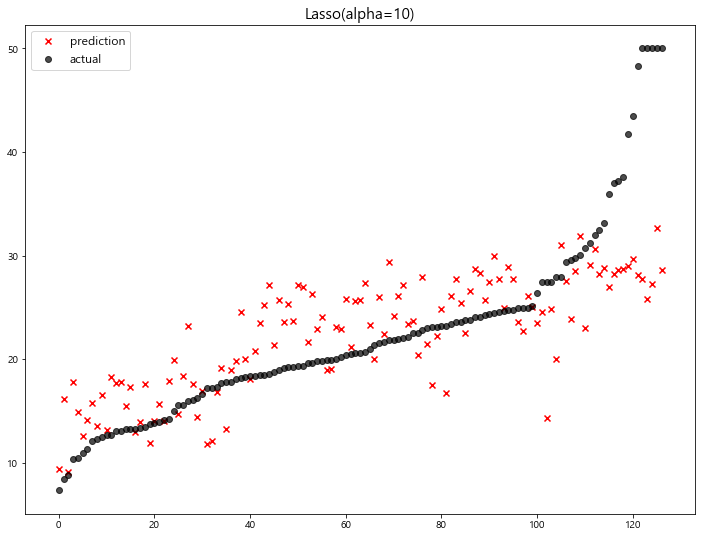
output_92_3

                model        mse
0    Lasso(alpha=100)  63.348818
1     Lasso(alpha=10)  42.436622
2    Ridge(alpha=100)  23.487453
3     Ridge(alpha=10)  22.793119
4    LinearRegression  22.770784
5  Ridge(alpha=0.001)  22.770117
6   Ridge(alpha=0.01)  22.764254
7    Ridge(alpha=0.1)  22.718126
8      Ridge(alpha=1)  22.690411

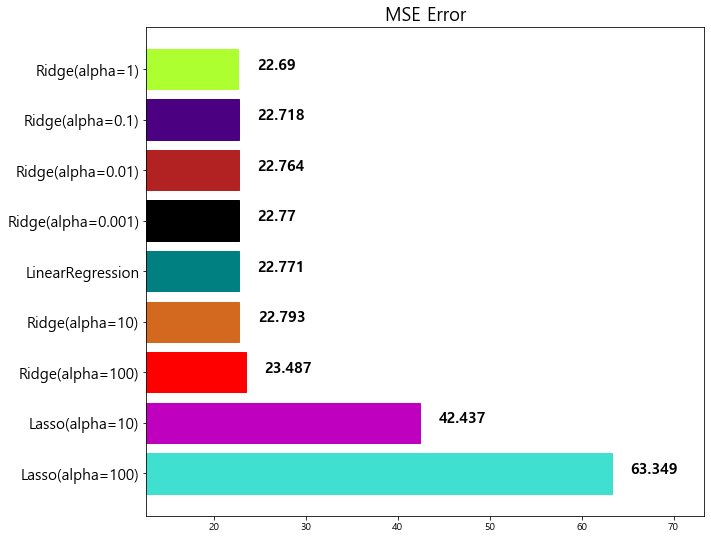
output_92_5

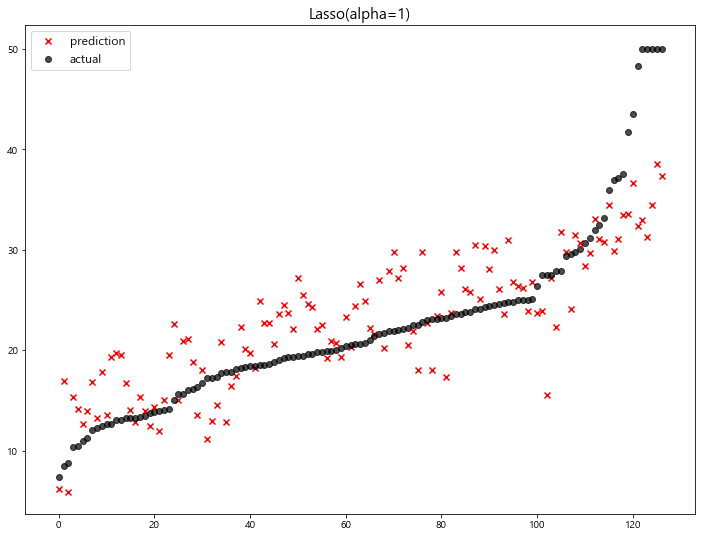
output_92_6

                model        mse
0    Lasso(alpha=100)  63.348818
1     Lasso(alpha=10)  42.436622
2      Lasso(alpha=1)  27.493672
3    Ridge(alpha=100)  23.487453
4     Ridge(alpha=10)  22.793119
5    LinearRegression  22.770784
6  Ridge(alpha=0.001)  22.770117
7   Ridge(alpha=0.01)  22.764254
8    Ridge(alpha=0.1)  22.718126
9      Ridge(alpha=1)  22.690411

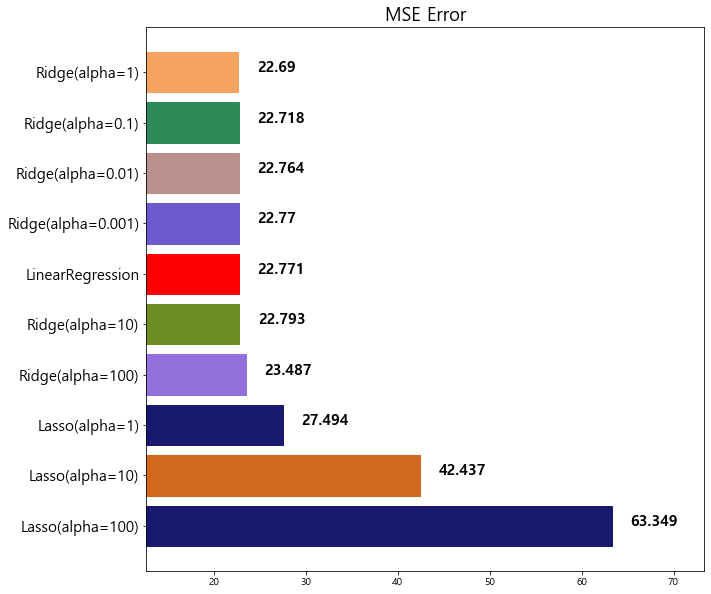
output_92_8

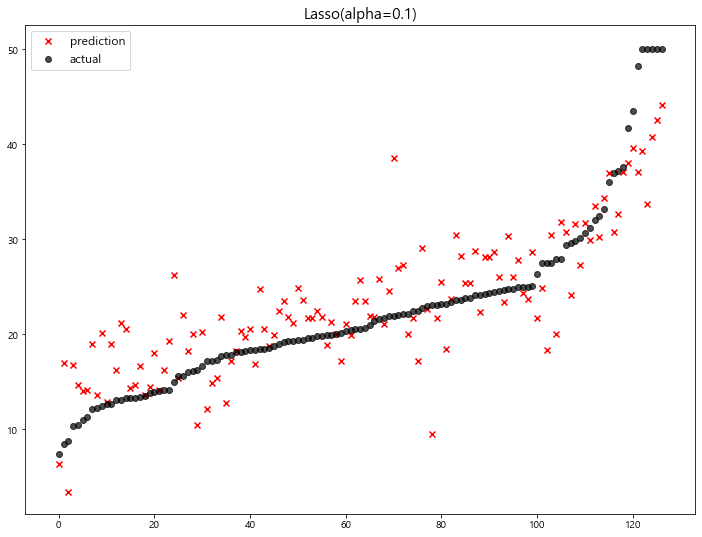
output_92_9

                 model        mse
0     Lasso(alpha=100)  63.348818
1      Lasso(alpha=10)  42.436622
2       Lasso(alpha=1)  27.493672
3     Ridge(alpha=100)  23.487453
4     Lasso(alpha=0.1)  22.979708
5      Ridge(alpha=10)  22.793119
6     LinearRegression  22.770784
7   Ridge(alpha=0.001)  22.770117
8    Ridge(alpha=0.01)  22.764254
9     Ridge(alpha=0.1)  22.718126
10      Ridge(alpha=1)  22.690411

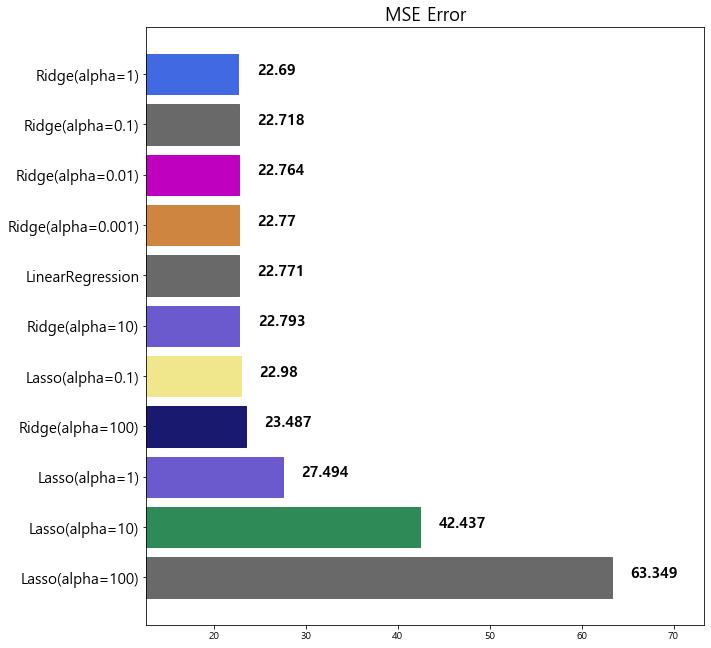
output_92_11

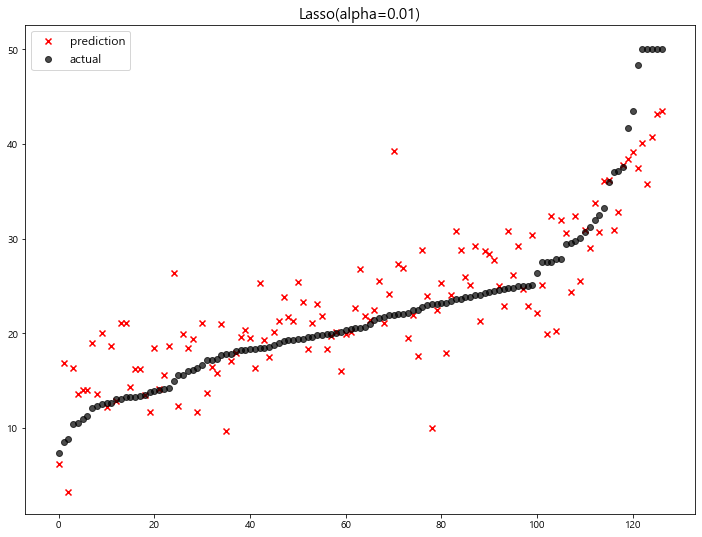
output_92_12

                 model        mse
0     Lasso(alpha=100)  63.348818
1      Lasso(alpha=10)  42.436622
2       Lasso(alpha=1)  27.493672
3     Ridge(alpha=100)  23.487453
4     Lasso(alpha=0.1)  22.979708
5      Ridge(alpha=10)  22.793119
6     LinearRegression  22.770784
7   Ridge(alpha=0.001)  22.770117
8    Ridge(alpha=0.01)  22.764254
9     Ridge(alpha=0.1)  22.718126
10      Ridge(alpha=1)  22.690411
11   Lasso(alpha=0.01)  22.635614

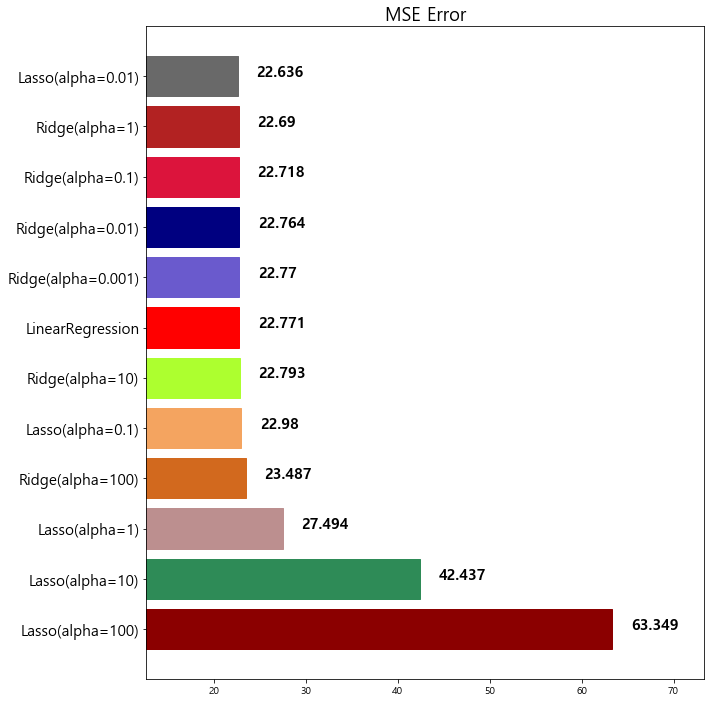
output_92_14

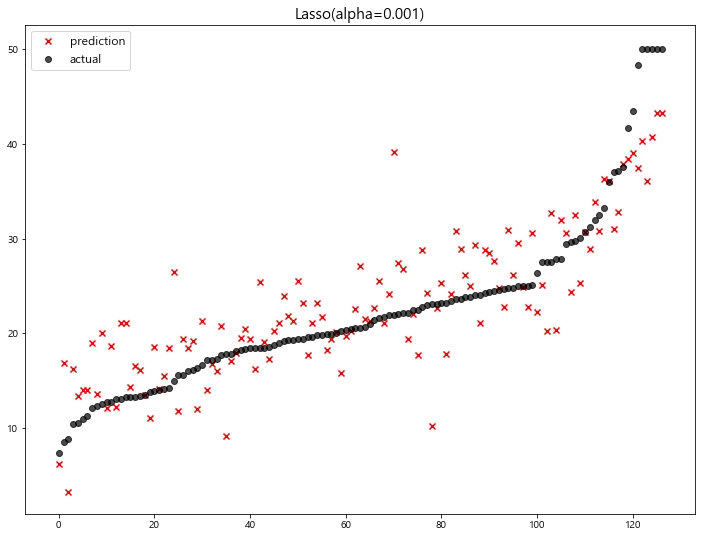
output_92_15

                 model        mse
0     Lasso(alpha=100)  63.348818
1      Lasso(alpha=10)  42.436622
2       Lasso(alpha=1)  27.493672
3     Ridge(alpha=100)  23.487453
4     Lasso(alpha=0.1)  22.979708
5      Ridge(alpha=10)  22.793119
6     LinearRegression  22.770784
7   Ridge(alpha=0.001)  22.770117
8    Ridge(alpha=0.01)  22.764254
9   Lasso(alpha=0.001)  22.753017
10    Ridge(alpha=0.1)  22.718126
11      Ridge(alpha=1)  22.690411
12   Lasso(alpha=0.01)  22.635614

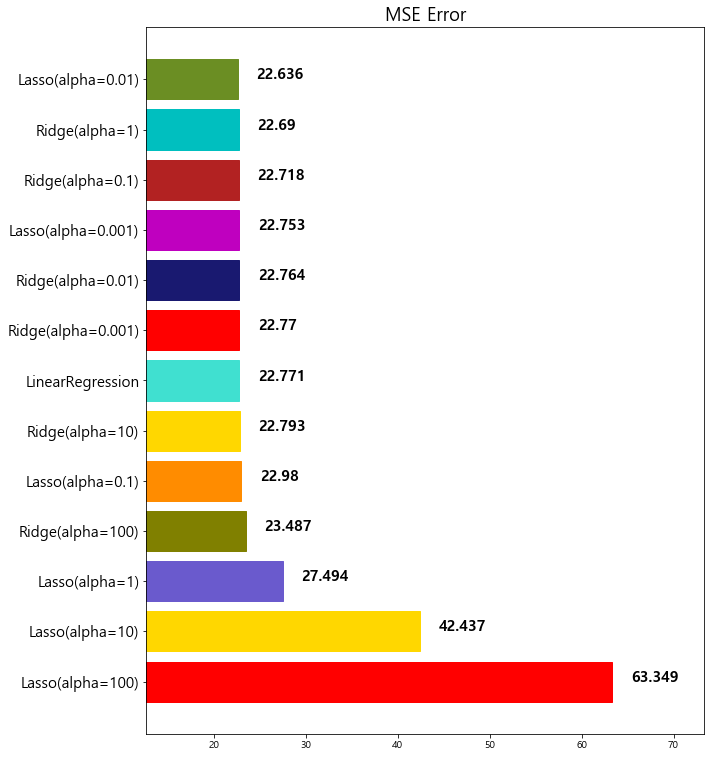
output_92_17

coefficients 값 확인

# alpha = 0.01
lasso_01 = Lasso(alpha=0.01)
lasso_01.fit(x_train, y_train)
lasso_pred_01 = lasso_01.predict(x_test)

# alpha = 100
lasso_100 = Lasso(alpha=100)
lasso_100.fit(x_train, y_train)
lasso_pred_100 = lasso_100.predict(x_test)

[alpha = 0.01]

1	x_train.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
       'PTRATIO', 'B', 'LSTAT'],
      dtype='object')

1	lasso_01.coef_

array([ -0.09427142,   0.04759954,   0.01255668,   3.08256139,
       -15.36800113,   4.07373679,  -0.00100439,  -1.40819927,
         0.27152905,  -0.0097157 ,  -0.84377679,   0.01249204,
        -0.52790174])

1	plot_coef(x_train.columns, lasso_01.coef_)

output_100_0

[alpha = 100]

1	x_train.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
       'PTRATIO', 'B', 'LSTAT'],
      dtype='object')

1	lasso_100.coef_

array([-0.        ,  0.        , -0.        ,  0.        , -0.        ,
        0.        , -0.        ,  0.        , -0.        , -0.02078349,
       -0.        ,  0.00644409, -0.        ])

1	plot_coef(x_train.columns, lasso_100.coef_)

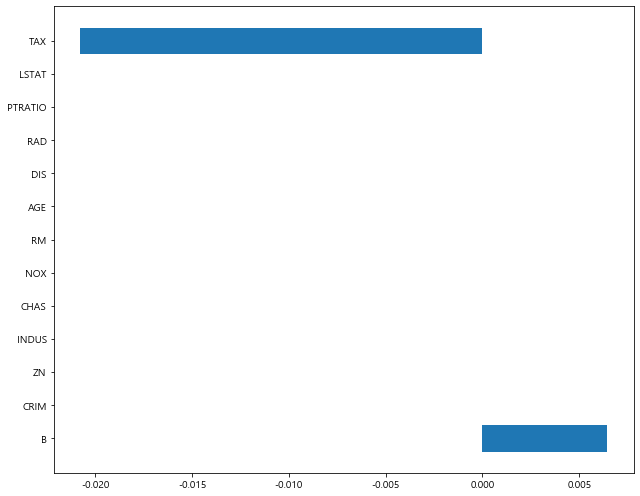
output_105_0

>> ElasticNet [Document]

1	from sklearn.linear_model import ElasticNet

예측 결과 확인

1	ratios = [0.2, 0.5, 0.8]

# alpha = 0.5 로 고정

for ratio in ratios:
    elasticnet = ElasticNet(alpha=0.1, l1_ratio=ratio)
    elasticnet.fit(x_train, y_train)
    elas_pred = elasticnet.predict(x_test)
    mse_eval('ElasticNet(l1_ratio={})'.format(ratio), y_test, elas_pred)

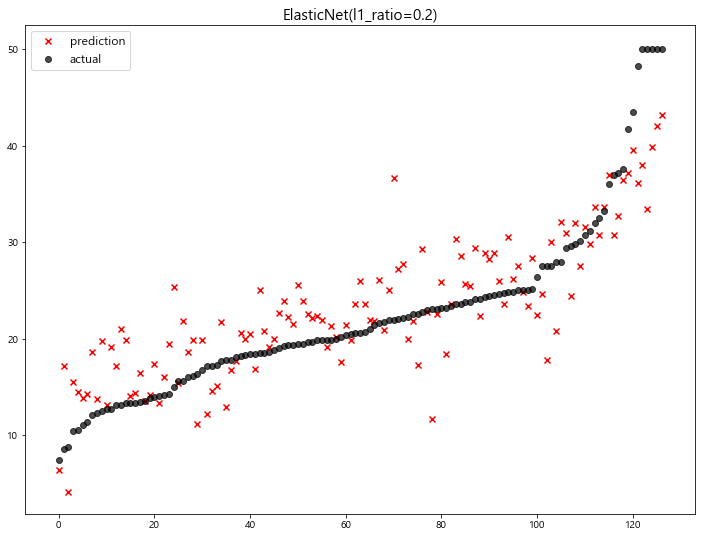
output_111_0

                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4           Lasso(alpha=0.1)  22.979708
5            Ridge(alpha=10)  22.793119
6           LinearRegression  22.770784
7         Ridge(alpha=0.001)  22.770117
8          Ridge(alpha=0.01)  22.764254
9         Lasso(alpha=0.001)  22.753017
10  ElasticNet(l1_ratio=0.2)  22.749018
11          Ridge(alpha=0.1)  22.718126
12            Ridge(alpha=1)  22.690411
13         Lasso(alpha=0.01)  22.635614

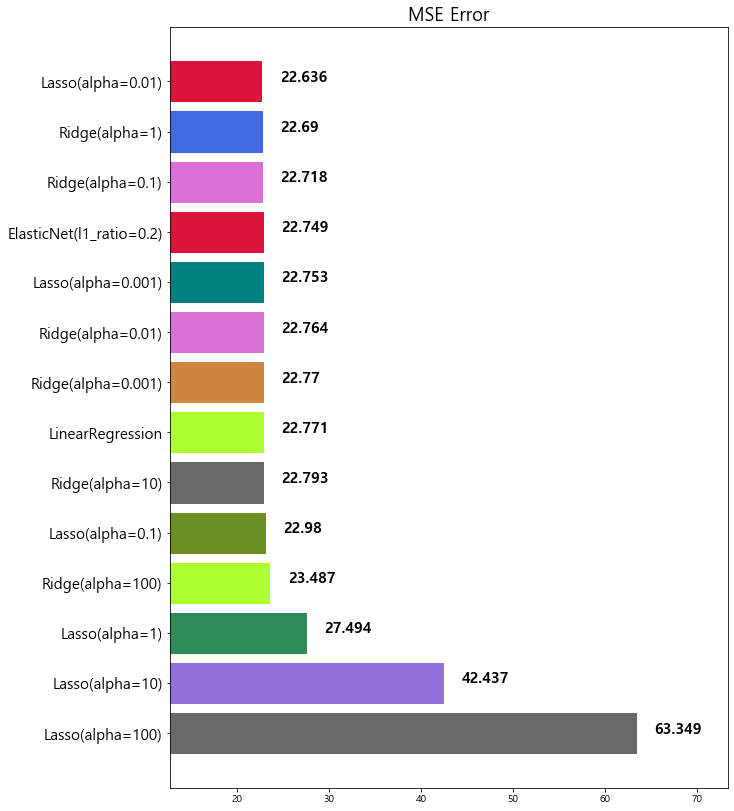
output_111_2

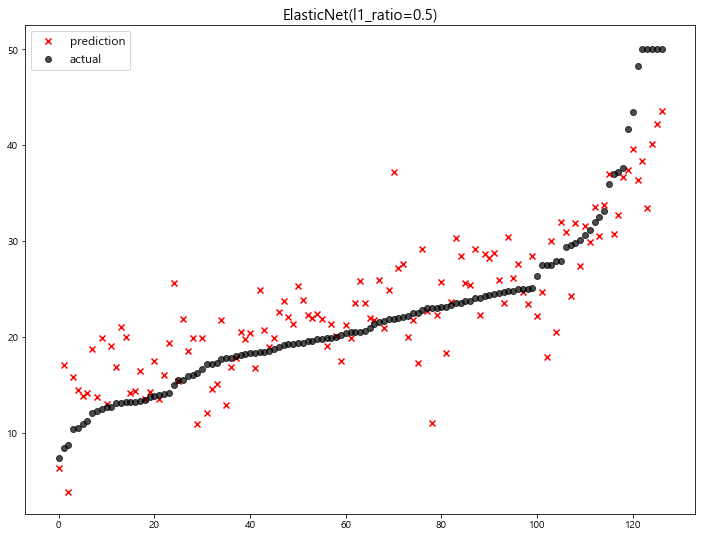
output_111_3

                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4           Lasso(alpha=0.1)  22.979708
5            Ridge(alpha=10)  22.793119
6   ElasticNet(l1_ratio=0.5)  22.787269
7           LinearRegression  22.770784
8         Ridge(alpha=0.001)  22.770117
9          Ridge(alpha=0.01)  22.764254
10        Lasso(alpha=0.001)  22.753017
11  ElasticNet(l1_ratio=0.2)  22.749018
12          Ridge(alpha=0.1)  22.718126
13            Ridge(alpha=1)  22.690411
14         Lasso(alpha=0.01)  22.635614

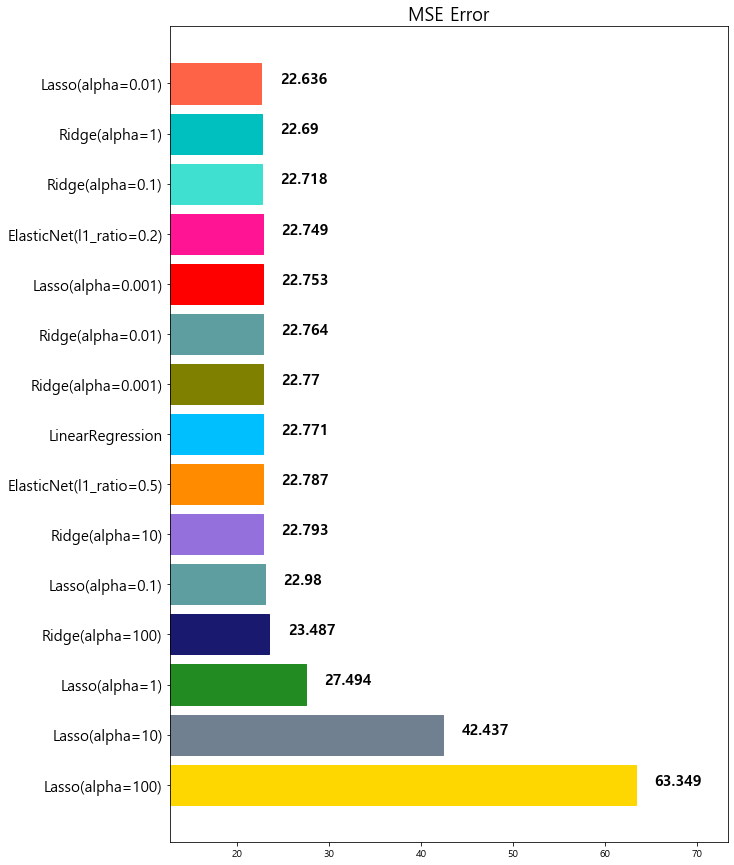
output_111_5

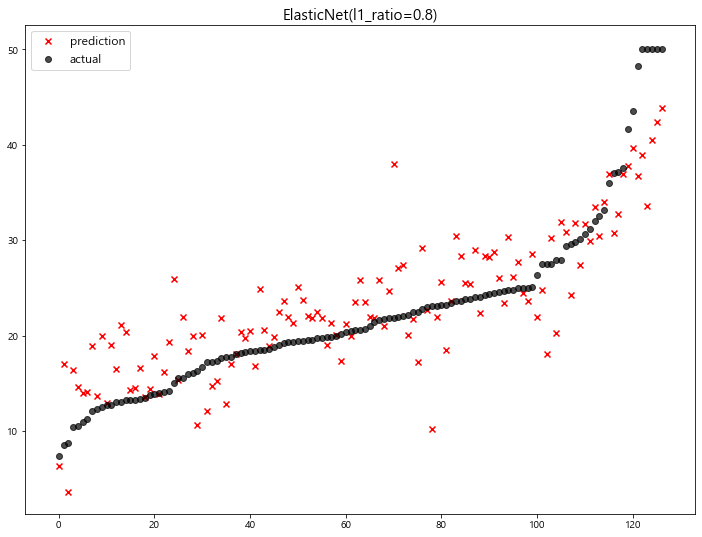
output_111_6

                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4           Lasso(alpha=0.1)  22.979708
5   ElasticNet(l1_ratio=0.8)  22.865628
6            Ridge(alpha=10)  22.793119
7   ElasticNet(l1_ratio=0.5)  22.787269
8           LinearRegression  22.770784
9         Ridge(alpha=0.001)  22.770117
10         Ridge(alpha=0.01)  22.764254
11        Lasso(alpha=0.001)  22.753017
12  ElasticNet(l1_ratio=0.2)  22.749018
13          Ridge(alpha=0.1)  22.718126
14            Ridge(alpha=1)  22.690411
15         Lasso(alpha=0.01)  22.635614

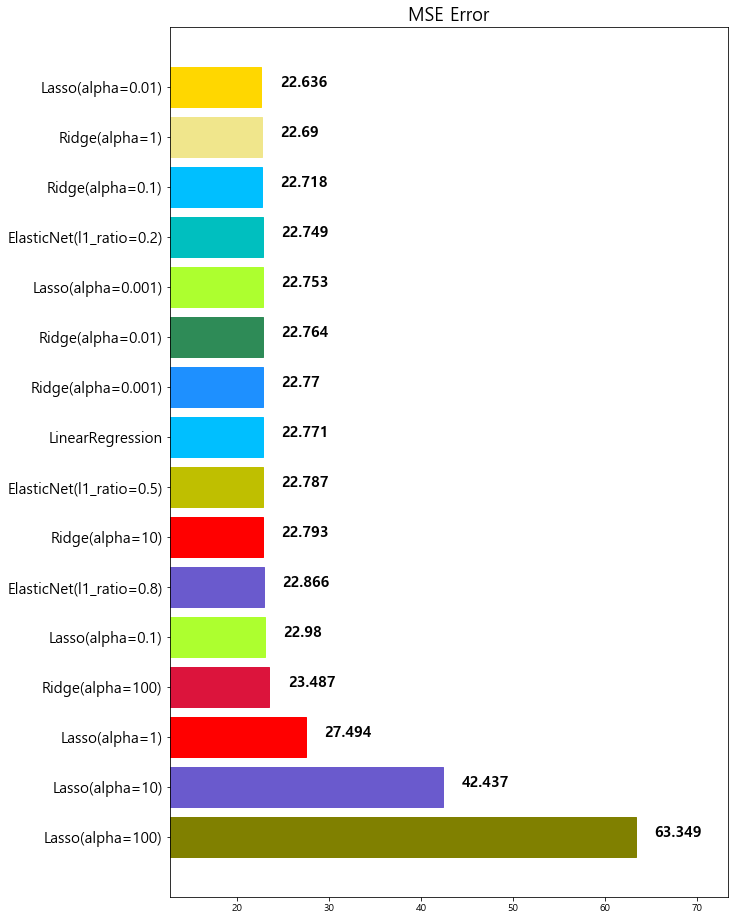
output_111_8

coefficients 값 확인

# ㅣ1_ratio = 0.2
elasticnet_2 = ElasticNet(alpha = 0.1, l1_ratio = 0.2)
elasticnet_2.fit(x_train, y_train)
elast_pred_2 = elasticnet_2.predict(x_test)

# l1_ratio = 0.8
elasticnet_8 = ElasticNet(alpha=0.1, l1_ratio = 0.8)
elasticnet_8.fit(x_train, y_train)
elast_pred_8 = elasticnet_8.predict(x_test)

[ l1_ratio = 0.2 ]

1	x_train.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
       'PTRATIO', 'B', 'LSTAT'],
      dtype='object')

1	elasticnet_2.coef_

array([-0.09297585,  0.05293361, -0.03950412,  1.30126199, -0.41996826,
        3.15838796, -0.00644646, -1.15290012,  0.25973467, -0.01231233,
       -0.77186571,  0.01201684, -0.60780037])

1	plot_coef(x_train.columns, elasticnet_2.coef_)

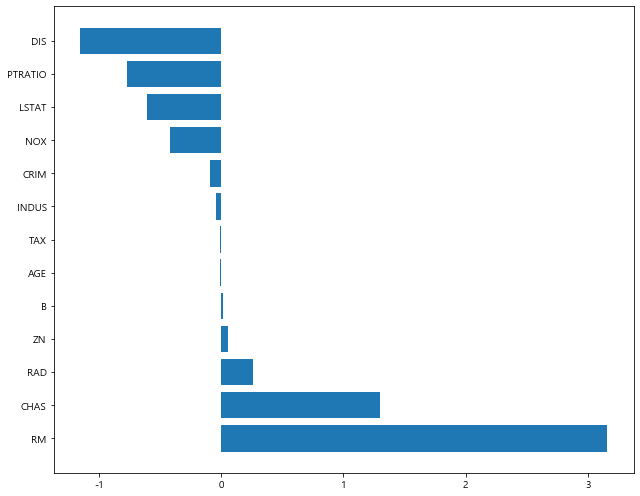
output_119_0

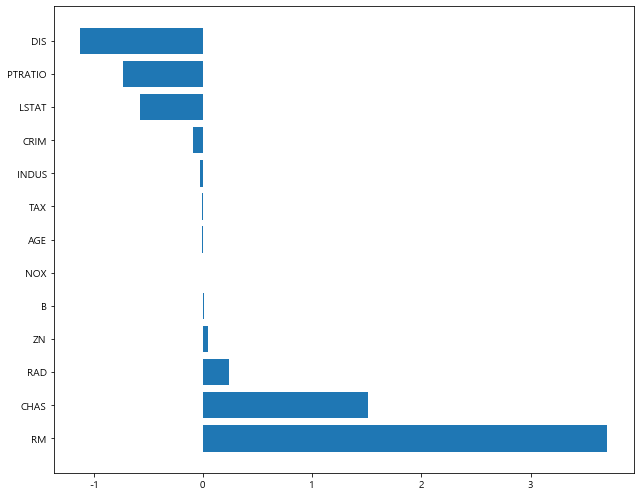
[ l1_ratio = 0.8 ]

1	x_train.columns

Index(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX',
       'PTRATIO', 'B', 'LSTAT'],
      dtype='object')

1	elasticnet_8.coef_

array([-0.08797633,  0.05035601, -0.03058513,  1.51071961, -0.        ,
        3.70247373, -0.01017259, -1.12431077,  0.24389841, -0.01189981,
       -0.73481448,  0.01259147, -0.573733  ])

1	plot_coef(x_train.columns, elasticnet_8.coef_)

output_124_0

4. Scaling

4-1. Scaler 소개

StandardScaler
MinMaxScaler
RobustScaler

1	from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler

1	x_train.describe()

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PTRATIO	B	LSTAT
count	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000	379.000000
mean	3.512192	11.779683	10.995013	0.076517	0.548712	6.266953	67.223483	3.917811	9.282322	404.680739	18.448549	357.048100	12.633773
std	8.338717	23.492842	6.792065	0.266175	0.115006	0.681796	28.563787	2.084167	8.583051	166.813256	2.154917	92.745266	7.259213
min	0.006320	0.000000	0.460000	0.000000	0.385000	3.561000	2.900000	1.129600	1.000000	188.000000	12.600000	2.520000	1.730000
25%	0.078910	0.000000	5.190000	0.000000	0.445000	5.876500	42.250000	2.150900	4.000000	278.000000	17.150000	375.425000	6.910000
50%	0.228760	0.000000	9.690000	0.000000	0.532000	6.208000	74.400000	3.414500	5.000000	330.000000	19.000000	392.110000	11.380000
75%	2.756855	19.000000	18.100000	0.000000	0.624000	6.611000	93.850000	5.400900	8.000000	666.000000	20.200000	396.260000	16.580000
max	73.534100	100.000000	27.740000	1.000000	0.871000	8.398000	100.000000	10.585700	24.000000	711.000000	22.000000	396.900000	37.970000

>> StandardScaler

평균(mean)을 0, 표준편차(std)를 1로 만들어 주는 scaler

1
2
3

std_scaler = StandardScaler()
std_scaled = std_scaler.fit_transform(x_train)
round(pd.DataFrame(std_scaled).describe(), 2)

	0	1	2	3	4	5	6	7	8	9	10	11	12
count	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00
mean	-0.00	0.00	0.00	-0.00	-0.00	-0.00	-0.00	0.00	-0.00	0.00	0.00	0.00	0.00
std	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00
min	-0.42	-0.50	-1.55	-0.29	-1.43	-3.97	-2.25	-1.34	-0.97	-1.30	-2.72	-3.83	-1.50
25%	-0.41	-0.50	-0.86	-0.29	-0.90	-0.57	-0.88	-0.85	-0.62	-0.76	-0.60	0.20	-0.79
50%	-0.39	-0.50	-0.19	-0.29	-0.15	-0.09	0.25	-0.24	-0.50	-0.45	0.26	0.38	-0.17
75%	-0.09	0.31	1.05	-0.29	0.66	0.51	0.93	0.71	-0.15	1.57	0.81	0.42	0.54
max	8.41	3.76	2.47	3.47	2.81	3.13	1.15	3.20	1.72	1.84	1.65	0.43	3.49

>> MinMaxScaler

min값과 max값을 0~1사이로 정규화 (Normalize)

1
2
3

minmax_scaler = MinMaxScaler()
minmax_scaled = minmax_scaler.fit_transform(x_train)
round(pd.DataFrame(minmax_scaled).describe(), 2)

	0	1	2	3	4	5	6	7	8	9	10	11	12
count	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00	379.00
mean	0.05	0.12	0.39	0.08	0.34	0.56	0.66	0.29	0.36	0.41	0.62	0.90	0.30
std	0.11	0.23	0.25	0.27	0.24	0.14	0.29	0.22	0.37	0.32	0.23	0.24	0.20
min	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
25%	0.00	0.00	0.17	0.00	0.12	0.48	0.41	0.11	0.13	0.17	0.48	0.95	0.14
50%	0.00	0.00	0.34	0.00	0.30	0.55	0.74	0.24	0.17	0.27	0.68	0.99	0.27
75%	0.04	0.19	0.65	0.00	0.49	0.63	0.94	0.45	0.30	0.91	0.81	1.00	0.41
max	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00	1.00

>> RobustScaler

중앙값(median)이 0, IQR(interquartile rage)이 1이 되도록 변환
outlier 처리에 유용

1
2
3

robust_scaler = RobustScaler()
robust_scaled = robust_scaler.fit_transform(x_train)
round(pd.DataFrame(robust_scaled).median(), 2)

0     0.0
1     0.0
2     0.0
3     0.0
4     0.0
5     0.0
6     0.0
7     0.0
8     0.0
9     0.0
10    0.0
11    0.0
12    0.0
dtype: float64

4-2. Scaling 후 모델 학습 – 파이프라인 활용

1	from sklearn.pipeline import make_pipeline

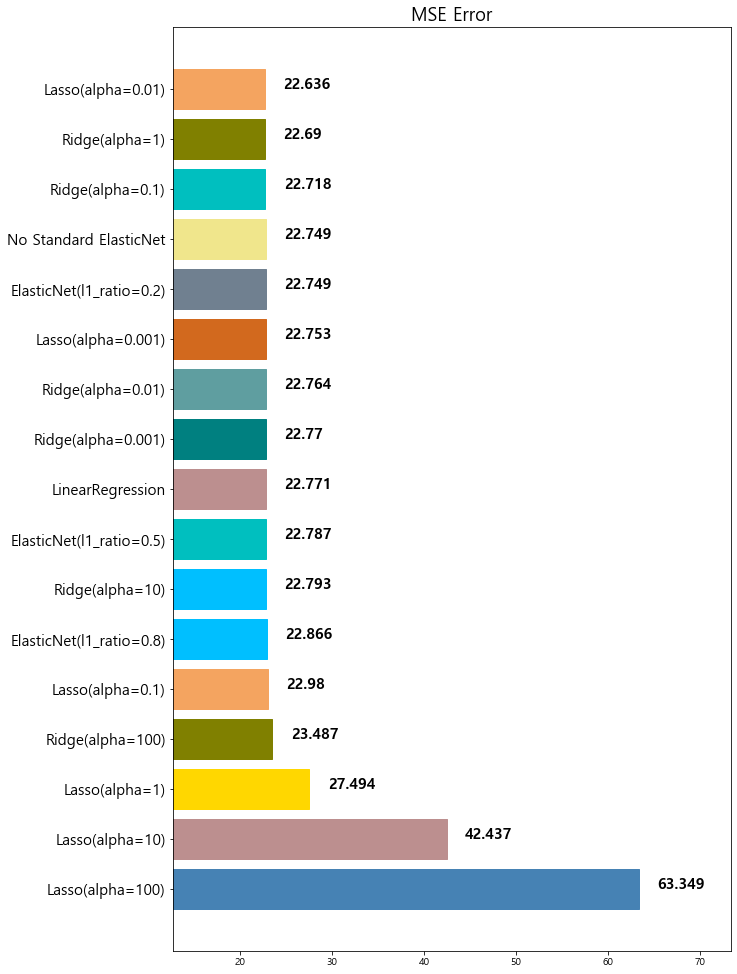
# elasticnet(alpha=0.1, l1_ratio=0.2) < without standard scaling >
elasticnet_no_scale = ElasticNet(alpha=0.1, l1_ratio=0.2)
no_scale_pred = elasticnet_no_scale.fit(x_train, y_train).predict(x_test)
mse_eval('No Standard ElasticNet', y_test, no_scale_pred)


# elasticnet(alpha=0.1, l1_ratio=0.2) < with standard scaling >
elasticnet_pipeline = make_pipeline(
    StandardScaler(),
    ElasticNet(alpha=0.1, l1_ratio=0.2)
)

with_scale_pred = elasticnet_pipeline.fit(x_train, y_train).predict(x_test)
mse_eval('With Standard ElasticNet', y_test, with_scale_pred)

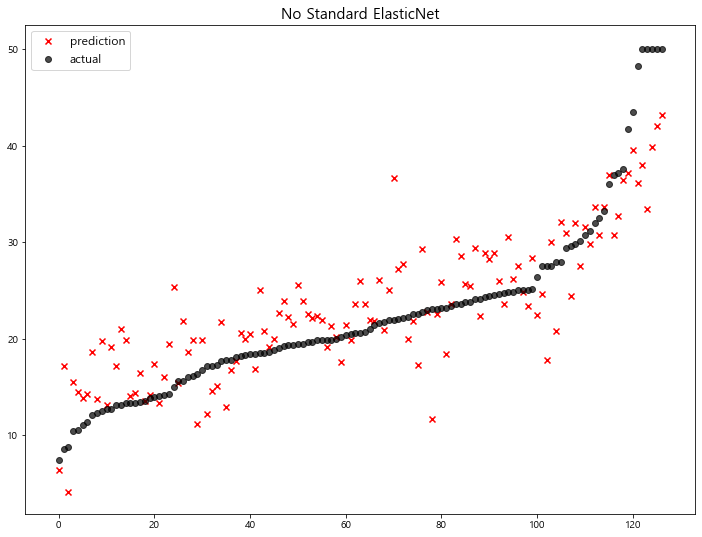
output_148_0

                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4           Lasso(alpha=0.1)  22.979708
5   ElasticNet(l1_ratio=0.8)  22.865628
6            Ridge(alpha=10)  22.793119
7   ElasticNet(l1_ratio=0.5)  22.787269
8           LinearRegression  22.770784
9         Ridge(alpha=0.001)  22.770117
10         Ridge(alpha=0.01)  22.764254
11        Lasso(alpha=0.001)  22.753017
12  ElasticNet(l1_ratio=0.2)  22.749018
13    No Standard ElasticNet  22.749018
14          Ridge(alpha=0.1)  22.718126
15            Ridge(alpha=1)  22.690411
16         Lasso(alpha=0.01)  22.635614

output_148_2

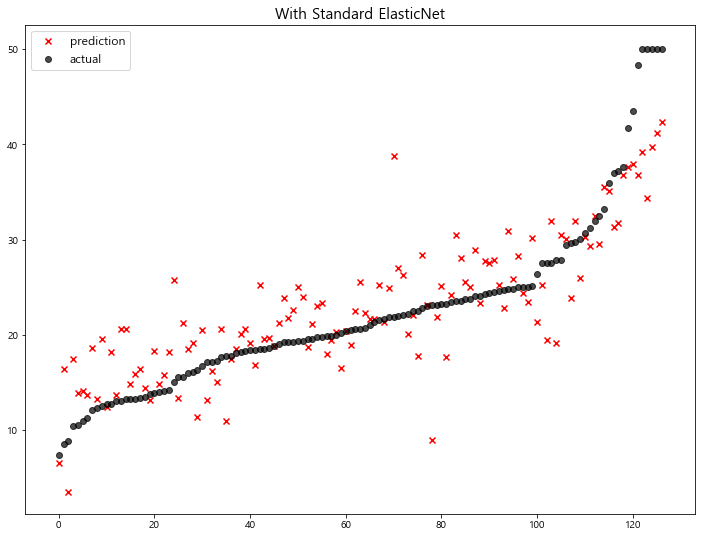
output_148_3

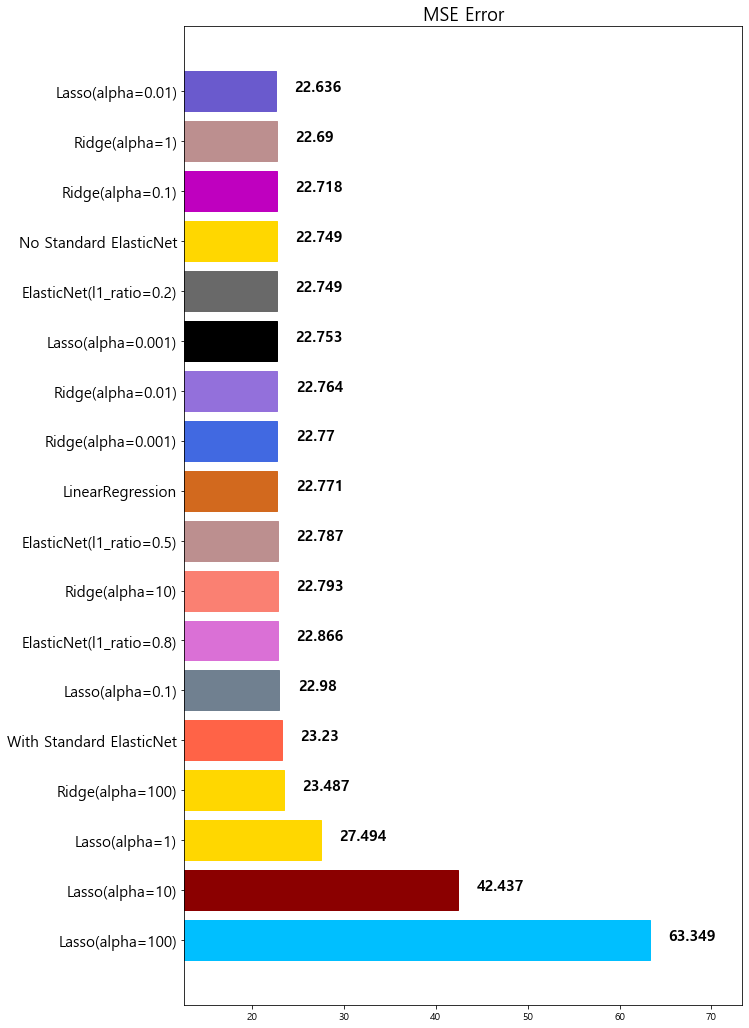
                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4   With Standard ElasticNet  23.230164
5           Lasso(alpha=0.1)  22.979708
6   ElasticNet(l1_ratio=0.8)  22.865628
7            Ridge(alpha=10)  22.793119
8   ElasticNet(l1_ratio=0.5)  22.787269
9           LinearRegression  22.770784
10        Ridge(alpha=0.001)  22.770117
11         Ridge(alpha=0.01)  22.764254
12        Lasso(alpha=0.001)  22.753017
13  ElasticNet(l1_ratio=0.2)  22.749018
14    No Standard ElasticNet  22.749018
15          Ridge(alpha=0.1)  22.718126
16            Ridge(alpha=1)  22.690411
17         Lasso(alpha=0.01)  22.635614

output_148_5

5. Polynomial Features

[Document]

다항식의 계수간 상호작용을 통해 새로운 feature를 생성한다.
예를 들면, [a, b] 2개의 feature가 존재한다고 가정하고,
degree=2로 설정한다면, polynomial features 는 [1, a, b, a^2, ab, b^2]가 돤다

1	from sklearn.preprocessing import PolynomialFeatures

Polynomial Features 생성

1	poly = PolynomialFeatures(degree=2, include_bias=False)

1 2	poly_features = poly.fit_transform(x_train)[0] poly_features

array([     0.12329   ,      0.        ,     10.01      ,      0.        ,
            0.547     ,      5.913     ,     92.9       ,      2.3534    ,
            6.        ,    432.        ,     17.8       ,    394.95      ,
           16.21      ,      0.01520042,      0.        ,      1.2341329 ,
            0.        ,      0.06743963,      0.72901377,     11.453641  ,
            0.29015069,      0.73974   ,     53.26128   ,      2.194562  ,
           48.6933855 ,      1.9985309 ,      0.        ,      0.        ,
            0.        ,      0.        ,      0.        ,      0.        ,
            0.        ,      0.        ,      0.        ,      0.        ,
            0.        ,      0.        ,    100.2001    ,      0.        ,
            5.47547   ,     59.18913   ,    929.929     ,     23.557534  ,
           60.06      ,   4324.32      ,    178.178     ,   3953.4495    ,
          162.2621    ,      0.        ,      0.        ,      0.        ,
            0.        ,      0.        ,      0.        ,      0.        ,
            0.        ,      0.        ,      0.        ,      0.299209  ,
            3.234411  ,     50.8163    ,      1.2873098 ,      3.282     ,
          236.304     ,      9.7366    ,    216.03765   ,      8.86687   ,
           34.963569  ,    549.3177    ,     13.9156542 ,     35.478     ,
         2554.416     ,    105.2514    ,   2335.33935   ,     95.84973   ,
         8630.41      ,    218.63086   ,    557.4       ,  40132.8       ,
         1653.62      ,  36690.855     ,   1505.909     ,      5.53849156,
           14.1204    ,   1016.6688    ,     41.89052   ,    929.47533   ,
           38.148614  ,     36.        ,   2592.        ,    106.8       ,
         2369.7       ,     97.26      , 186624.        ,   7689.6       ,
       170618.4       ,   7002.72      ,    316.84      ,   7030.11      ,
          288.538     , 155985.5025    ,   6402.1395    ,    262.7641    ])

1	x_train.iloc[0]

CRIM         0.12329
ZN           0.00000
INDUS       10.01000
CHAS         0.00000
NOX          0.54700
RM           5.91300
AGE         92.90000
DIS          2.35340
RAD          6.00000
TAX        432.00000
PTRATIO     17.80000
B          394.95000
LSTAT       16.21000
Name: 112, dtype: float64

Polynomial Features + Standard Scaling 후 모델 학습

poly_pipeline = make_pipeline(
    PolynomialFeatures(degree=2, include_bias=False),
    StandardScaler(),
    ElasticNet(alpha=0.1, l1_ratio=0.2)
)

1	poly_pred = poly_pipeline.fit(x_train, y_train).predict(x_test)

D:\Anaconda\lib\site-packages\sklearn\linear_model\_coordinate_descent.py:476: ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Duality gap: 32.61172784964583, tolerance: 3.2374824854881266
  positive)

1	mse_eval('Poly ElasticNet', y_test, poly_pred)

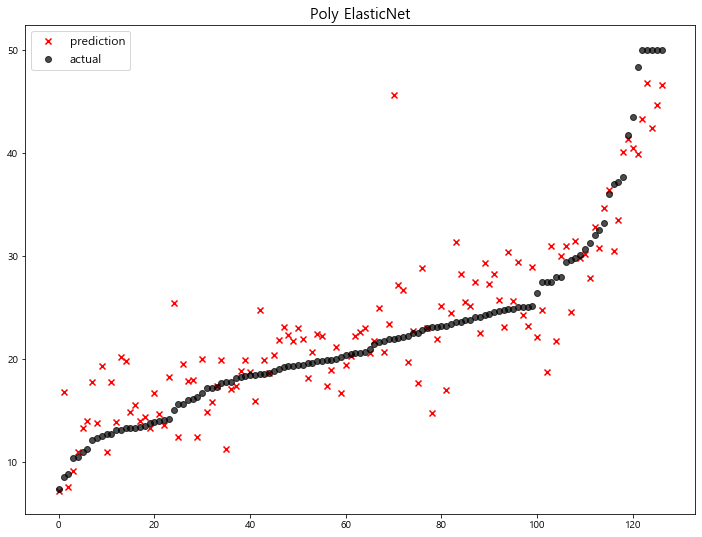
output_163_0

                       model        mse
0           Lasso(alpha=100)  63.348818
1            Lasso(alpha=10)  42.436622
2             Lasso(alpha=1)  27.493672
3           Ridge(alpha=100)  23.487453
4   With Standard ElasticNet  23.230164
5           Lasso(alpha=0.1)  22.979708
6   ElasticNet(l1_ratio=0.8)  22.865628
7            Ridge(alpha=10)  22.793119
8   ElasticNet(l1_ratio=0.5)  22.787269
9           LinearRegression  22.770784
10        Ridge(alpha=0.001)  22.770117
11         Ridge(alpha=0.01)  22.764254
12        Lasso(alpha=0.001)  22.753017
13  ElasticNet(l1_ratio=0.2)  22.749018
14    No Standard ElasticNet  22.749018
15          Ridge(alpha=0.1)  22.718126
16            Ridge(alpha=1)  22.690411
17         Lasso(alpha=0.01)  22.635614
18           Poly ElasticNet  17.526214

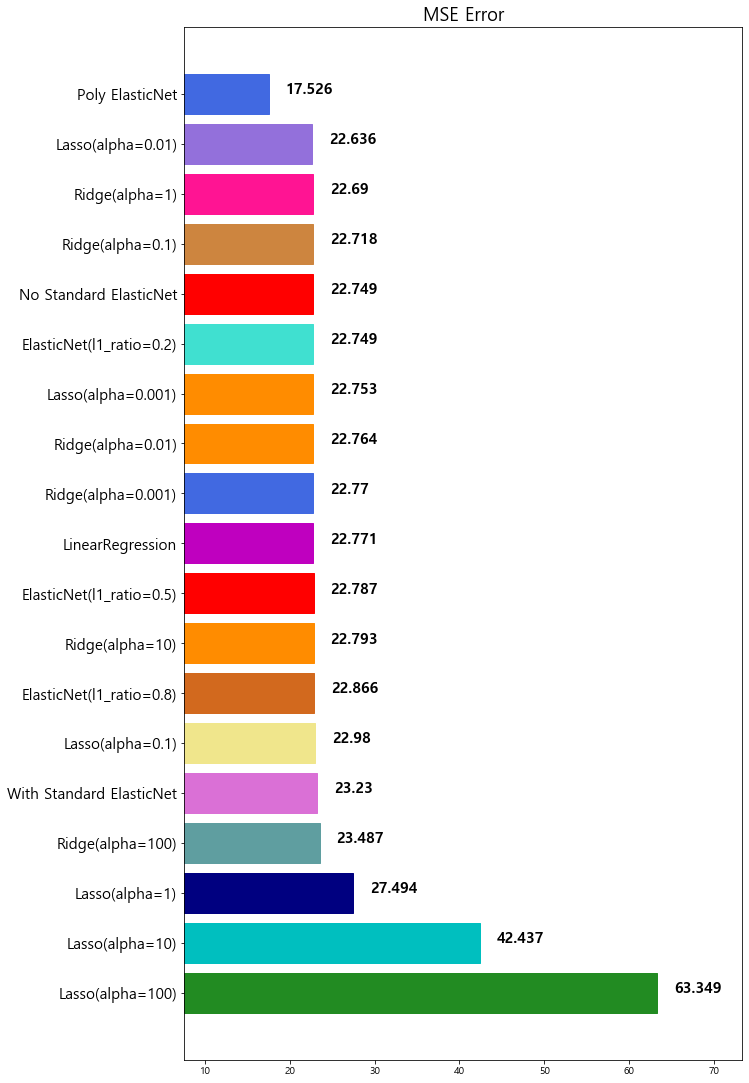
output_163_2