비지도 학습 (Unsupervised Learning)


1
from IPython.display import Image

1. 비지도 학습의 개요

비지도 학습 (Unsupervised Learning)은 기계 학습의 일종으로, 데이터가 어떻게 구성되어 있는지를 알아내는 문제의 범주에 속한다. 이 방법은 지도 학습 (Supervised Learning) 혹은 강화 학습 (Reinforcement Learning)과는 달리 입력값에 대한 목표치가 주어지지 않는다

  • 차원 축소: PCA, LDA, SVD

  • 군집화: KMeans Clustering, DBSCAN

  • 군집화 평가


2. 차원 축소

  • feature의 갯수를 줄이는 것을 뛰어 넘어, 특징을 추출하는 역할응 하기도 함
  • 계산 비용을 감소하는 효과
  • 전반적인 데이터에 대한 이해도를 높이는 효과
1
2
3
4
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn import datasets
import pandas as pd

2-1. 데이터 로드 (iris 데이터)

1
iris = datasets.load_iris()
1
data = iris['data']
1
data[:5]
array([[5.1, 3.5, 1.4, 0.2],
       [4.9, 3. , 1.4, 0.2],
       [4.7, 3.2, 1.3, 0.2],
       [4.6, 3.1, 1.5, 0.2],
       [5. , 3.6, 1.4, 0.2]])

1
df = pd.DataFrame(data, columns = iris['feature_names'])
1
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm)
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2
3 4.6 3.1 1.5 0.2
4 5.0 3.6 1.4 0.2 
1
df['target'] = iris['target']
1
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0

2-2. PCA 차원 축소

참고: PCA 원리 관련 블로그

주성분 분석 (PCA, Principal Component Analysis) 는 선형 차원 축소 기법이다. 매우 인기 있게 사용되는 차원 축소 기법중 하나다.

PCA는 먼저 데이터에 가장 가까운 초평면(hyperplane)을 구한 다음, 데이터를 이 초평면에 투영(projection)시킨다. 주요 특징 중의 하나는 분산(variance)을 촤대한 보존한다는 점이다.

  • 분산 보존

    PCA는 데이터의 분산이 최대가 되는 축을 찾는다. 즉, 원본 데이터셋과 투영된 데이터셋 간의 평균제곱거리를 최소화하는 축을 찾는다.

  • PCA 실현 과정

    1. 학습 데이터셋에서 분산이 최대인 축(axis)을 찾는다
    2. 이렇게 찾은 첫 번째 축과 직교(orthogonal)하면서 분산이 최대인 두 번째 축을 찾는다
    3. 첫 번째 축과 두 번째 축에 직교하고 분산을 최대한 보존하는 세 번째 축을 찾는다
    4. 1~3과 같은 방법으로 데이터셋의 차원(특성 수)만큼의 축을 찾는다

    이렇게 i-번째 축을 정의하는 **단위 벡터(unit vector)**를 i-번째 주성분(PC, Principle Component)이라고 한다.


>> sklearn에서 실현

[sklearn.decomposition.PCA] Documnet

  • n_components에 1보다 작은 값을 넣으면, 분산을 기준으로 차원 축소

  • n_components에 1보다 큰 값을 넣으면, 해당 값을 기준으로 feature를 축소


(1) 주성분 2개로 지정 (n_components = 2)

1
from sklearn.decomposition import PCA
1
2
3
4
5
6
7
8
# 모델 선언
pca = PCA(n_components=2)

# data scaling
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])

# PCA 실행
pca_data = pca.fit_transform(data_scaled)
1
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0 
1
data_scaled[:5]
array([[-0.90068117,  1.01900435, -1.34022653, -1.3154443 ],
       [-1.14301691, -0.13197948, -1.34022653, -1.3154443 ],
       [-1.38535265,  0.32841405, -1.39706395, -1.3154443 ],
       [-1.50652052,  0.09821729, -1.2833891 , -1.3154443 ],
       [-1.02184904,  1.24920112, -1.34022653, -1.3154443 ]])

1
pca_data[:5]
array([[-2.26470281,  0.4800266 ],
       [-2.08096115, -0.67413356],
       [-2.36422905, -0.34190802],
       [-2.29938422, -0.59739451],
       [-2.38984217,  0.64683538]])

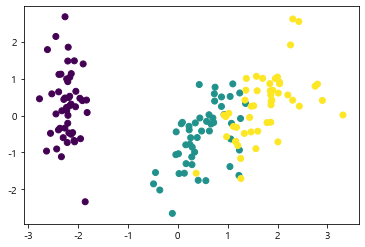
주성분에 따른 데이터 시각화

1
2
3
4
5
import matplotlib.pyplot as plt
from matplotlib import cm
import seaborn as sns

%matplotlib inline
1
plt.scatter(pca_data[:, 0], pca_data[:, 1], c=df['target']) # c: color 기준
<matplotlib.collections.PathCollection at 0x201028bf148>

output_39_1


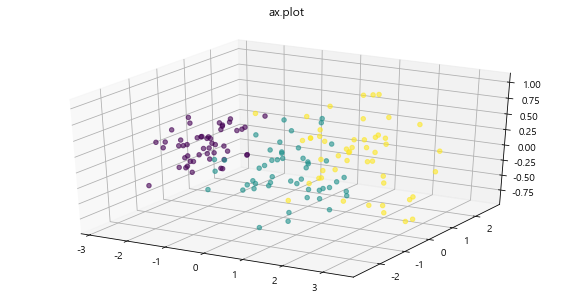
(2) 분산을 기준으로 차원축소 (n_components < 1)

1
2
3
pca2 = PCA(n_components=0.99)
pca_data2 = pca2.fit_transform(data_scaled)
pca_data2[:5]
array([[-2.26470281,  0.4800266 , -0.12770602],
       [-2.08096115, -0.67413356, -0.23460885],
       [-2.36422905, -0.34190802,  0.04420148],
       [-2.29938422, -0.59739451,  0.09129011],
       [-2.38984217,  0.64683538,  0.0157382 ]])

1
2
3
4
5
6
7
8
9
10
11
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

fig = plt.figure(figsize=(10, 5))
ax = fig.add_subplot(111, projection='3d')  # Axe3D object

sample_size = 50
ax.scatter(pca_data2[:,0], pca_data2[:,1], pca_data2[:,2], alpha=0.6, c=df['target'])
plt.savefig('./tmp.svg')
plt.title('ax.plot')
plt.show()

output_43_0


2-3. LDA 차원 축소

참고 블로그:

  1. 차원 축소 - LDA(Linear Discriminant Analysis) 개요
  2. 머신러닝 기초9 - LDA (Linear Discriminant Analysis)

LDA (Linear Discriminant Analysis): 선형 판별 분석법 (PCA와 유사)

LDA는 클래스(Class)분리를 최대화하는 축을 찾기 위해 클래스 간 분산(between-class scatter)과 내분 분산(within-class scatter)의 비율을 최대화하는 방식으로 차원을 축소함.

즉, 클래스 간 분산은 최대한 크게 가져가고, 클래스 내부의 분산은 최대한 작게 가져가는 방식이다.


>> sklearn에서 실현

1
2
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
1
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0 
1
2
3
4
5
6
7
8
# 모델 선언
lda = LinearDiscriminantAnalysis(n_components=2)

# data scaling
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])

# LDA 실행
lda_data = lda.fit_transform(data_scaled, df['target'])
1
lda_data[:5]
array([[-8.06179978,  0.30042062],
       [-7.12868772, -0.78666043],
       [-7.48982797, -0.26538449],
       [-6.81320057, -0.67063107],
       [-8.13230933,  0.51446253]])

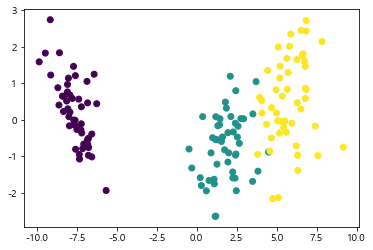
시각화

1
2
# LDA
plt.scatter(lda_data[:,0], lda_data[:,1], c=df['target'])
<matplotlib.collections.PathCollection at 0x20102cd5608>

output_57_1

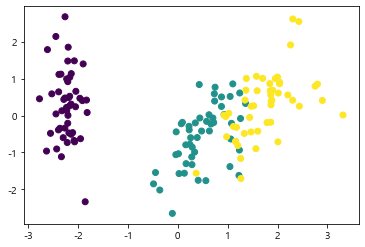
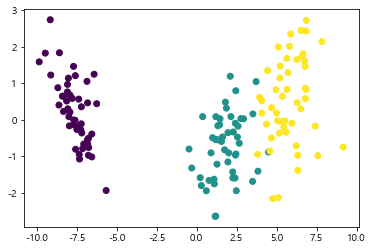
PCA 결과와 비교

1
2
# PCA
plt.scatter(pca_data[:,0], pca_data[:,1], c=df['target'])
<matplotlib.collections.PathCollection at 0x20102ba6908>

output_59_1


2-4. SVD (특이값 분해)

위키문서

SVD (Singular Value Decomposition):

  • 특이값 분해 기법이다
  • PCA와 유사한 차원 축소 기법이다
  • scikit-learn 패키지에서는 truncated SVD (aka LSA)을 사용한다
  • 상품의 추천 시스템에도 활용되어지는 알고리즘 (추천시스템)
1
from sklearn.decomposition import TruncatedSVD
1
df.head()
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.1 3.5 1.4 0.2 0
1 4.9 3.0 1.4 0.2 0
2 4.7 3.2 1.3 0.2 0
3 4.6 3.1 1.5 0.2 0
4 5.0 3.6 1.4 0.2 0 
1
2
3
svd = TruncatedSVD(n_components = 2)
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])
svd_data = svd.fit_transform(data_scaled)
1
svd_data[:5]
array([[-2.26470281,  0.4800266 ],
       [-2.08096115, -0.67413356],
       [-2.36422905, -0.34190802],
       [-2.29938422, -0.59739451],
       [-2.38984217,  0.64683538]])

시각화

1
2
# SVD
plt.scatter(svd_data[:,0], svd_data[:,1], c=df['target'])
<matplotlib.collections.PathCollection at 0x20102b2ed08>

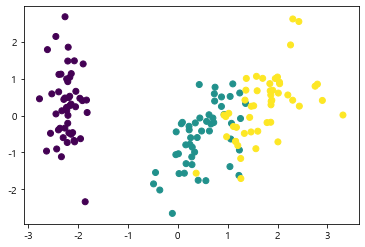
output_71_1

PCA & LDA와 비교

1
2
# PCA
plt.scatter(pca_data[:,0], pca_data[:,1], c=df['target'])
<matplotlib.collections.PathCollection at 0x20102ad7d88>

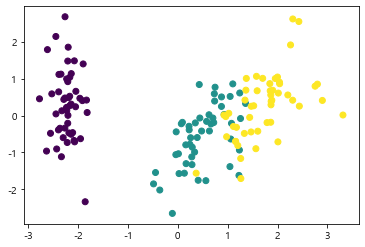
output_73_1

1
2
# LDA
plt.scatter(lda_data[:,0], lda_data[:,1], c=df['target'])
<matplotlib.collections.PathCollection at 0x20102d43e08>

output_74_1



3. 군집화

3-1. K-Means Clustering

위키문서

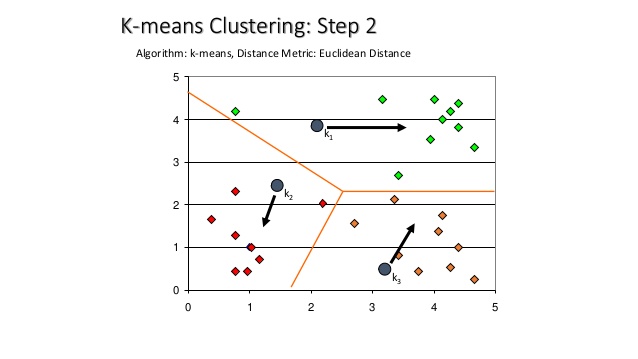
군집화에서 가장 대중적으로 사용되는 알고리즘이다. centroid라는 중점을 기준으로 가강 가까운 포인트를 선택하는 군집화 기법이다

원리: 주어진 데이터를 k개의 cluster로 묶는 방식, 거리 차이의 분산을 최소화하는 방식으로 동작.

1
Image('https://image.slidesharecdn.com/patternrecognitionbinoy-06-kmeansclustering-160317135729/95/pattern-recognition-binoy-k-means-clustering-13-638.jpg')

output_81_0


사용되는 예제

  • 스팸 문자 분류
  • 뉴스 기사 분류

[sklearn.cluster.KMeans] Document

1
from sklearn.cluster import KMeans
1
2
3
kmeans = KMeans(n_clusters=3)
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])
cluster_data = kmeans.fit_transform(data_scaled)
1
cluster_data[:5]
array([[3.12119834, 0.21295824, 3.98940603],
       [2.6755083 , 0.99604549, 4.01793312],
       [2.97416665, 0.65198444, 4.19343668],
       [2.88014429, 0.9034561 , 4.19784749],
       [3.30022609, 0.40215457, 4.11157152]])

1
kmeans.labels_
array([1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 1, 1, 1, 2, 2, 2, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 2,
       0, 0, 0, 0, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0, 0, 0, 0, 0, 2, 2, 0,
       0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 0, 2, 2, 2, 2, 0, 2, 2, 2,
       2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 0, 2, 0, 2, 2, 0, 2, 2, 2, 2, 2,
       2, 0, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 0])

1
sns.countplot(kmeans.labels_)
<matplotlib.axes._subplots.AxesSubplot at 0x201043c7fc8>

output_88_1

1
sns.countplot(df['target'])
<matplotlib.axes._subplots.AxesSubplot at 0x2010301bec8>

output_89_1


Hyper-parameter Tuning

1
kmeans
KMeans(algorithm='auto', copy_x=True, init='k-means++', max_iter=300,
       n_clusters=3, n_init=10, n_jobs=None, precompute_distances='auto',
       random_state=None, tol=0.0001, verbose=0)

1
2
3
4
# max_iter: maximum number of iterations for a single run
kmeans2 = KMeans(n_clusters=3, max_iter=500)
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])
cluster_data2 = kmeans2.fit_transform(data_scaled)
1
sns.countplot(kmeans2.labels_)
<matplotlib.axes._subplots.AxesSubplot at 0x20105525688>

output_94_1


3-2. DBSCAN

밀도 기반 클러스터링
(DBSCAN: Dencity-Based Spatial Clustering of Applications with Noise)

  • 밀도가 높은 부분을 클러스터링 하는 방식
  • 어느 점을 기준으로 반경 x내에 점이 n개 이상 있으면 하나의 군집으로 인식하는 방식
  • KMeans 에서는 n_cluster의 갯수를 반드시 지정해 주어야 하나, DBSCAN에서는 필요없음
  • 기하학적인 clustering도 잘 찾아냄
1
Image('https://image.slidesharecdn.com/pydatanyc2015-151119175854-lva1-app6891/95/pydata-nyc-2015-automatically-detecting-outliers-with-datadog-26-638.jpg')

output_98_0


[sklearn.cluster.DBSCAN] Document

주의: 변환 시 fit_transform()대신 fit_predict() 를 쓴다

1
from sklearn.cluster import DBSCAN
1
2
3
4
5
# eps: The maximum distance between two samples for one to be considered as in the neighborhoood of the other
dbscan = DBSCAN(eps=0.7, min_samples=2)
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])
dbscan_data = dbscan.fit_predict(data_scaled)
dbscan_data
array([ 0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,
        0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,  0,
        0,  0,  0,  0,  0,  0,  0, -1,  0,  0,  0,  0,  0,  0,  0,  0,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,
        1,  1,  1,  1, -1,  1,  1, -1,  1,  1,  1,  1,  1,  1,  1,  2,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  2,  1,  1,  1,  1,
        1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1,  1],
      dtype=int64)

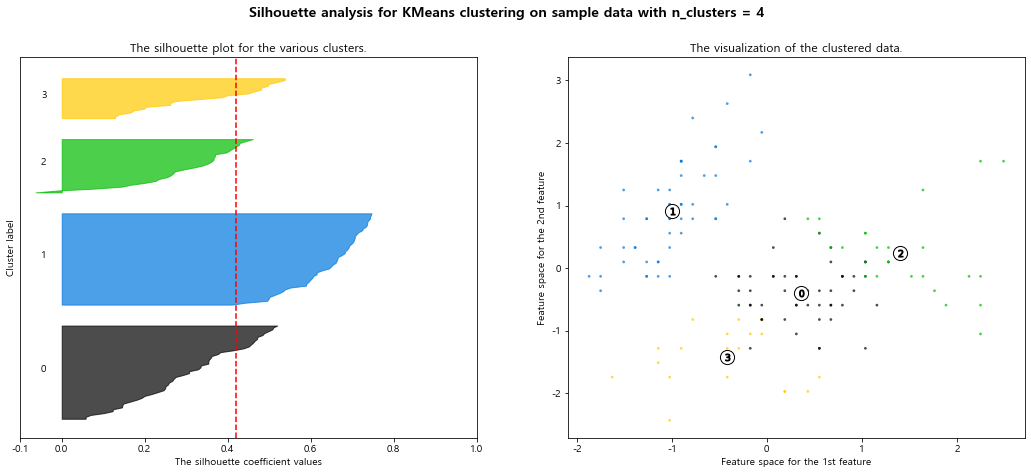
3-3. 실루엣 스코어 (군집화 평가)

클러스터링의 품질을 정량적으로 평가해 주는 지표

  • 1: 클러스터링의 품질이 좋다
  • 0: 클러스터링의 품질이 안좋다 (클러스터링의 의미 없음)
  • 음수: 잘못 분류됨
1
from sklearn.metrics import silhouette_samples, silhouette_score
1
2
3
data_scaled = StandardScaler().fit_transform(df.loc[:, 'sepal length (cm)' : 'petal width (cm)'])
score = silhouette_score(data_scaled, kmeans.labels_)
score
0.45994823920518635

1
2
samples = silhouette_samples(data_scaled, kmeans.labels_)
samples[:5]
array([0.73419485, 0.56827391, 0.67754724, 0.62050159, 0.72847412])

silhouette analysis 시각화 Document

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
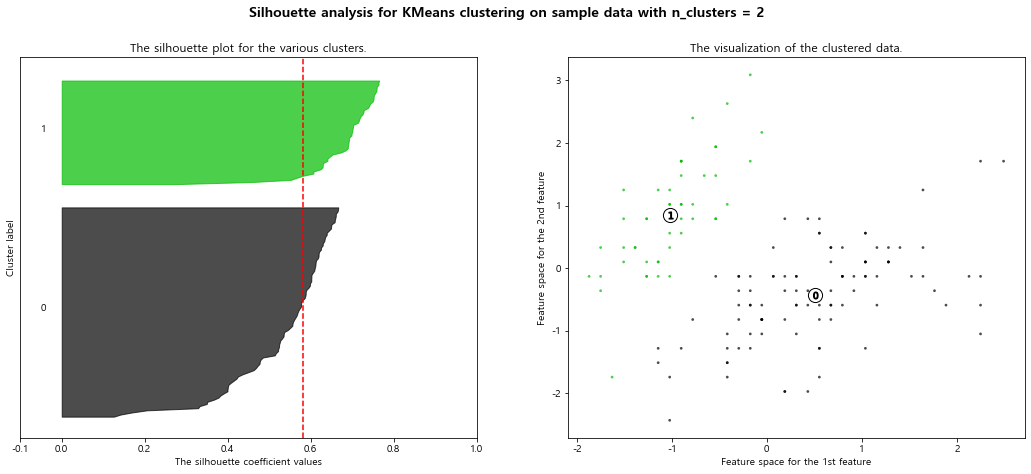
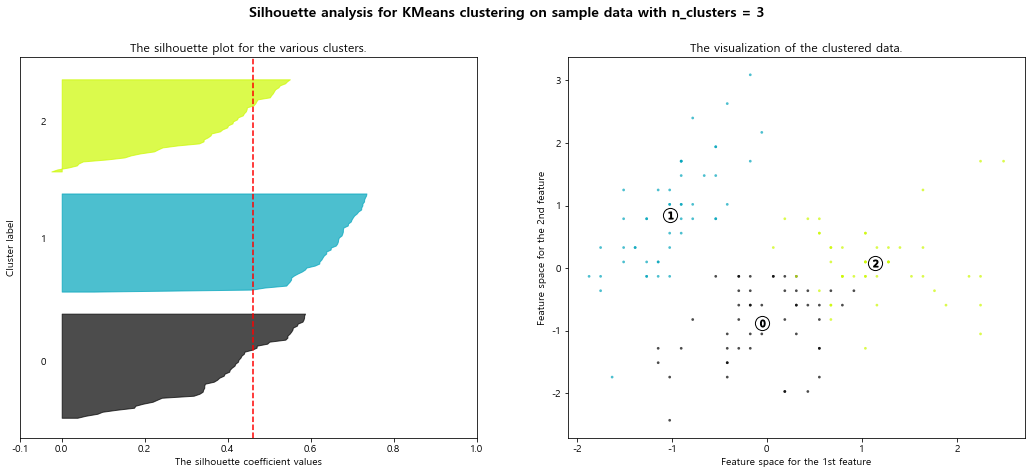
86
def plot_silhouette(X, num_cluesters):
    for n_clusters in num_cluesters:
        # Create a subplot with 1 row and 2 columns
        fig, (ax1, ax2) = plt.subplots(1, 2)
        fig.set_size_inches(18, 7)

        # The 1st subplot is the silhouette plot
        # The silhouette coefficient can range from -1, 1 but in this example all
        # lie within [-0.1, 1]
        ax1.set_xlim([-0.1, 1])
        # The (n_clusters+1)*10 is for inserting blank space between silhouette
        # plots of individual clusters, to demarcate them clearly.
        ax1.set_ylim([0, len(X) + (n_clusters + 1) * 10])
    
        # Initialize the clusterer with n_clusters value and a random generator
        # seed of 10 for reproducibility.
        clusterer = KMeans(n_clusters=n_clusters, random_state=10)
        cluster_labels = clusterer.fit_predict(X)
    
        # The silhouette_score gives the average value for all the samples.
        # This gives a perspective into the density and separation of the formed
        # clusters
        silhouette_avg = silhouette_score(X, cluster_labels)
        print("For n_clusters =", n_clusters,
              "The average silhouette_score is :", silhouette_avg)
    
        # Compute the silhouette scores for each sample
        sample_silhouette_values = silhouette_samples(X, cluster_labels)
    
        y_lower = 10
        for i in range(n_clusters):
            # Aggregate the silhouette scores for samples belonging to
            # cluster i, and sort them
            ith_cluster_silhouette_values = \
                sample_silhouette_values[cluster_labels == i]
    
            ith_cluster_silhouette_values.sort()
    
            size_cluster_i = ith_cluster_silhouette_values.shape[0]
            y_upper = y_lower + size_cluster_i
    
            color = cm.nipy_spectral(float(i) / n_clusters)
            ax1.fill_betweenx(np.arange(y_lower, y_upper),
                              0, ith_cluster_silhouette_values,
                              facecolor=color, edgecolor=color, alpha=0.7)
    
            # Label the silhouette plots with their cluster numbers at the middle
            ax1.text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))
    
            # Compute the new y_lower for next plot
            y_lower = y_upper + 10  # 10 for the 0 samples
    
        ax1.set_title("The silhouette plot for the various clusters.")
        ax1.set_xlabel("The silhouette coefficient values")
        ax1.set_ylabel("Cluster label")
    
        # The vertical line for average silhouette score of all the values
        ax1.axvline(x=silhouette_avg, color="red", linestyle="--")
    
        ax1.set_yticks([])  # Clear the yaxis labels / ticks
        ax1.set_xticks([-0.1, 0, 0.2, 0.4, 0.6, 0.8, 1])
    
        # 2nd Plot showing the actual clusters formed
        colors = cm.nipy_spectral(cluster_labels.astype(float) / n_clusters)
        ax2.scatter(X[:, 0], X[:, 1], marker='.', s=30, lw=0, alpha=0.7,
                    c=colors, edgecolor='k')
    
        # Labeling the clusters
        centers = clusterer.cluster_centers_
        # Draw white circles at cluster centers
        ax2.scatter(centers[:, 0], centers[:, 1], marker='o',
                    c="white", alpha=1, s=200, edgecolor='k')
    
        for i, c in enumerate(centers):
            ax2.scatter(c[0], c[1], marker='$%d$' % i, alpha=1,
                        s=50, edgecolor='k')
    
        ax2.set_title("The visualization of the clustered data.")
        ax2.set_xlabel("Feature space for the 1st feature")
        ax2.set_ylabel("Feature space for the 2nd feature")
    
        plt.suptitle(("Silhouette analysis for KMeans clustering on sample data "
                      "with n_clusters = %d" % n_clusters),
                     fontsize=14, fontweight='bold')
    
        plt.show()
1
plot_silhouette(data_scaled, [2, 3, 4, 5])
For n_clusters = 2 The average silhouette_score is : 0.5817500491982808

output_112_1

For n_clusters = 3 The average silhouette_score is : 0.45994823920518635

output_112_3

For n_clusters = 4 The average silhouette_score is : 0.4188923398171004

output_112_5

For n_clusters = 5 The average silhouette_score is : 0.34551099599809465

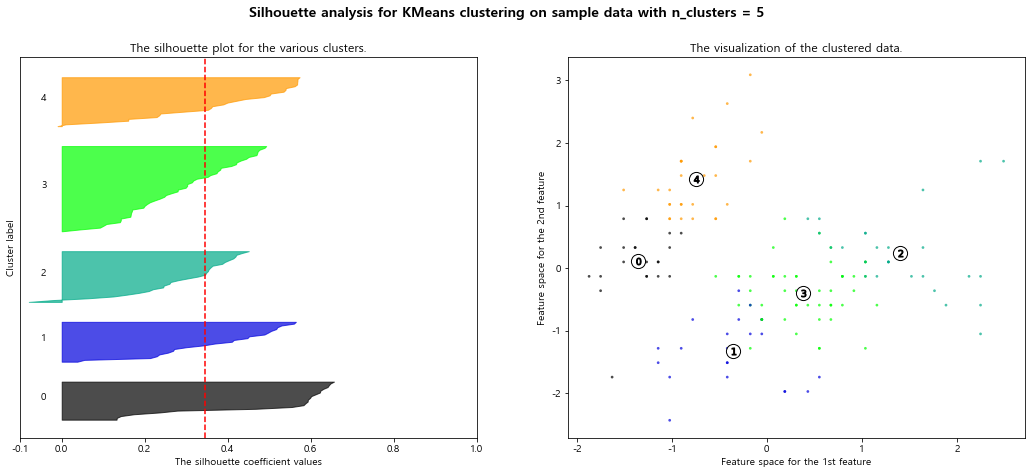
output_112_7

  • 빨간 점선은 평균 실루엣 계수를 의미함