앙상블 (Ensemble)


머신러닝 앙상블이란 여러 개의 머신러닝 모델을 이용해 최적의 답을 찾아내는 기법이다.
(여러 모델을 이용하여 데이터를 학습하고, 모든 모델의 예측결과를 평균하여 예측)


앙상블 기법의 종류

  • 보팅 (Voting): 투표를 통해 결과 도출
  • 배깅 (Bagging): 샘플 중복 생성을 통해 결과 도출
  • 부스팅 (Boosting): 이전 오차를 보완하면서 가중치 부여
  • 스태킹 (Stacking): 여러 모델을 기반으로 예측된 결과를 통해 meta 모델이 다시 한번 예측

참고자료 (블로그)

0. 데이터 셋

1
2
3
4
5
import pandas as pd
import numpy as np
from IPython.display import Image

np.set_printoptions(suppress=True) # If True, print floating point numbers instead of scientific notation
1
from sklearn.datasets import load_boston

0-1. 데이터 로드

1
data = load_boston()
1
print(data['DESCR'])
.. _boston_dataset:

Boston house prices dataset
---------------------------

**Data Set Characteristics:**  

    :Number of Instances: 506 

    :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

    :Attribute Information (in order):
        - CRIM     per capita crime rate by town
        - ZN       proportion of residential land zoned for lots over 25,000 sq.ft.
        - INDUS    proportion of non-retail business acres per town
        - CHAS     Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
        - NOX      nitric oxides concentration (parts per 10 million)
        - RM       average number of rooms per dwelling
        - AGE      proportion of owner-occupied units built prior to 1940
        - DIS      weighted distances to five Boston employment centres
        - RAD      index of accessibility to radial highways
        - TAX      full-value property-tax rate per $10,000
        - PTRATIO  pupil-teacher ratio by town
        - B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
        - LSTAT    % lower status of the population
        - MEDV     Median value of owner-occupied homes in $1000's

    :Missing Attribute Values: None

    :Creator: Harrison, D. and Rubinfeld, D.L.

This is a copy of UCI ML housing dataset.
https://archive.ics.uci.edu/ml/machine-learning-databases/housing/

​

This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.

The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978.   Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980.   N.B. Various transformations are used in the table on
pages 244-261 of the latter.

The Boston house-price data has been used in many machine learning papers that address regression
problems.   
     
.. topic:: References

   - Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
   - Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.

​


0-2. 데이터프레임 만들기

1
2
df = pd.DataFrame(data['data'], columns = data['feature_names'])
df['MEDV'] = data['target']
1
df.head()
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT MEDV
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2

컬럼 소게 (feature 13 + target 1):

  • CRIM: 범죄율

  • ZN: 25,000 square feet 당 주거용 토지의 비율

  • INDUS: 비소매(non-retail) 비즈니스 면적 비율

  • CHAS: 찰스 강 더미 변수 (통로가 하천을 향하면 1; 그렇지 않으면 0)

  • NOX: 산화 질소 농도 (천만 분의 1)

  • RM:주거 당 평균 객실 수

  • AGE: 1940 년 이전에 건축된 자가 소유 점유 비율

  • DIS: 5 개의 보스턴 고용 센터까지의 가중 거리

  • RAD: 고속도로 접근성 지수

  • TAX: 10,000 달러 당 전체 가치 재산 세율

  • PTRATIO 도시 별 학생-교사 비율

  • B: 1000 (Bk-0.63) ^ 2 여기서 Bk는 도시 별 검정 비율입니다.

  • LSTAT: 인구의 낮은 지위

  • MEDV: 자가 주택의 중앙값 (1,000 달러 단위)


1. Training set / Test set 나누기

1
from sklearn.model_selection import train_test_split
1
x_train, x_test, y_train, y_test = train_test_split(df.drop('MEDV', 1), df['MEDV'], random_state=23)
1
x_train.shape, y_train.shape
((379, 13), (379,))

1
x_test.shape, y_test.shape
((127, 13), (127,))

2. 평가 지표 만들기

2-1. 평가 지표

(1) MAE (Mean Absolute Error)

MAE (평균 절대 오차): 에측값과 실제값의 차이의 절대값에 대하여 평균을 낸 것

MAE=1n∑i=1n∣yi−yi^∣MAE = \frac{1}{n} \sum_{i=1}^n \left\vert y_i - \widehat{y_i} \right\vert

(2) MSE (Mean Squared Error)

MSE (평균 제곱 오차): 예측값과 실제값의 차이의 제곱에 대하여 평균을 낸 것

MSE=1n∑i=1n(yi−yi^)2MSE = \frac{1}{n} \sum_{i=1}^n \left( y_i - \widehat{y_i} \right)^2

(3) RMSE (Root Mean Squared Error)

RMSE (평균 제곱근 오차): 예측값과 실제값의 차이의 제곱에 대하여 평균을 낸 뒤 루트를 씌운 것

RMSE=1n∑i=1n(yi−yi^)2RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^n \left( y_i - \widehat{y_i} \right)^2}


2-2. 모델 성능 확인을 위한 함수

1
2
# sklearn 평가지표 활용
from sklearn.metrics import mean_absolute_error, mean_squared_error
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
import matplotlib.pyplot as plt
import seaborn as sns

my_predictions = {}

colors = ['r', 'c', 'm', 'y', 'k', 'khaki', 'teal', 'orchid', 'sandybrown',
          'greenyellow', 'dodgerblue', 'deepskyblue', 'rosybrown', 'firebrick',
          'deeppink', 'crimson', 'salmon', 'darkred', 'olivedrab', 'olive', 
          'forestgreen', 'royalblue', 'indigo', 'navy', 'mediumpurple', 'chocolate',
          'gold', 'darkorange', 'seagreen', 'turquoise', 'steelblue', 'slategray', 
          'peru', 'midnightblue', 'slateblue', 'dimgray', 'cadetblue', 'tomato'
         ]

# prediction plot
def plot_predictions(name_, actual, pred):
    df = pd.DataFrame({'actual': y_test, 'prediction': pred})
    df = df.sort_values(by='actual').reset_index(drop=True)

    plt.figure(figsize=(12, 9))
    plt.scatter(df.index, df['prediction'], marker='x', color='r')
    plt.scatter(df.index, df['actual'], alpha=0.7, marker='o', color='black')
    plt.title(name_, fontsize=15)
    plt.legend(['prediction', 'actual'], fontsize=12)
    plt.show()

# evaluation plot
def mse_eval(name_, actual, pred):
    global predictions
    global colors

    plot_predictions(name_, actual, pred)

    mse = mean_squared_error(actual, pred)
    my_predictions[name_] = mse

    y_value = sorted(my_predictions.items(), key=lambda x: x[1], reverse=True)
    
    df = pd.DataFrame(y_value, columns=['model', 'mse'])
    print(df)
    min_ = df['mse'].min() - 10
    max_ = df['mse'].max() + 10
    
    length = len(df)
    
    plt.figure(figsize=(10, length))
    ax = plt.subplot()
    ax.set_yticks(np.arange(len(df)))
    ax.set_yticklabels(df['model'], fontsize=15)
    bars = ax.barh(np.arange(len(df)), df['mse'])
    
    for i, v in enumerate(df['mse']):
        idx = np.random.choice(len(colors))
        bars[i].set_color(colors[idx])
        ax.text(v + 2, i, str(round(v, 3)), color='k', fontsize=15, fontweight='bold')
        
    plt.title('MSE Error', fontsize=18)
    plt.xlim(min_, max_)
    
    plt.show()

# remove model
def remove_model(name_):
    global my_predictions
    try:
        del my_predictions[name_]
    except KeyError:
        return False
    return True


# coefficients visulization
def plot_coef(columns, coef):
    coef_df = pd.DataFrame(list(zip(columns, coef)))
    coef_df.columns=['feature', 'coef']
    coef_df = coef_df.sort_values('coef', ascending=False).reset_index(drop=True)
    
    fig, ax = plt.subplots(figsize=(9, 7))
    ax.barh(np.arange(len(coef_df)), coef_df['coef'])
    idx = np.arange(len(coef_df))
    ax.set_yticks(idx)
    ax.set_yticklabels(coef_df['feature'])
    fig.tight_layout()
    plt.show()



3. 단일 회귀 모델 (지난 시간)

1
2
3
4
5
6
7
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import PolynomialFeatures

(1) Linear Regression

1
2
3
4
linear_reg = LinearRegression(n_jobs=-1)
linear_reg.fit(x_train, y_train)
linear_pred = linear_reg.predict(x_test)
mse_eval('LinearRegression', y_test, linear_pred)

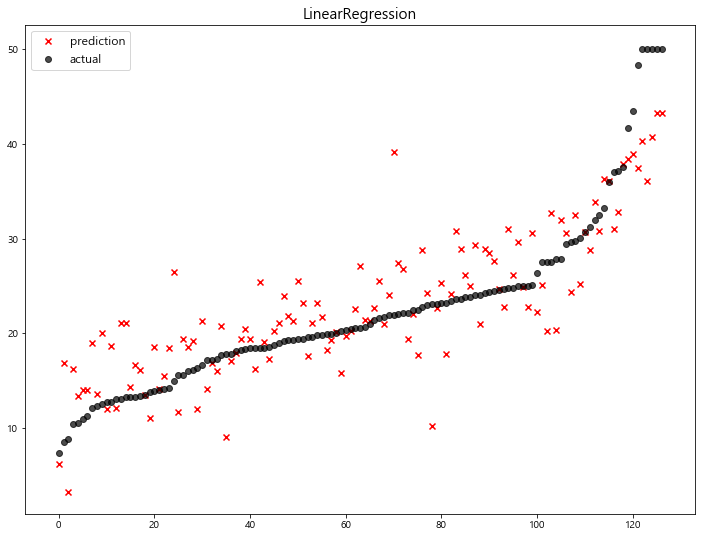
output_43_0

              model        mse
0  LinearRegression  22.770784

output_43_2


(2) Ridge

1
2
3
4
ridge = Ridge(alpha=1)
ridge.fit(x_train, y_train)
ridge_pred = ridge.predict(x_test)
mse_eval('Ridge(alpha=1)', y_test, ridge_pred)

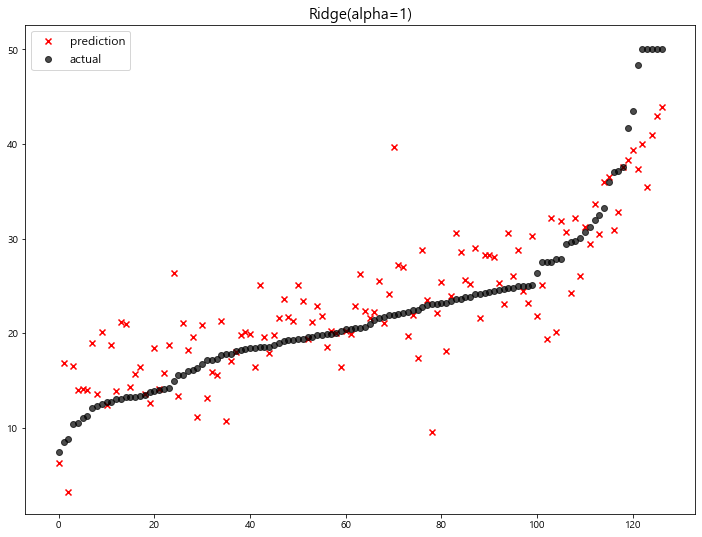
output_46_0

              model        mse
0  LinearRegression  22.770784
1    Ridge(alpha=1)  22.690411

output_46_2


(3) LASSO

1
2
3
4
lasso = Lasso(alpha=0.01)
lasso.fit(x_train, y_train)
lasso_pred = lasso.predict(x_test)
mse_eval('Lasso(alpha=0.01)', y_test, lasso_pred)

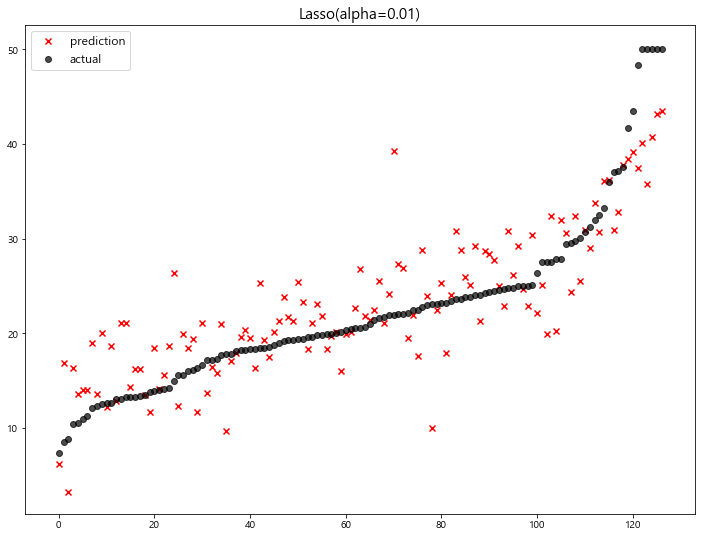
output_49_0

               model        mse
0   LinearRegression  22.770784
1     Ridge(alpha=1)  22.690411
2  Lasso(alpha=0.01)  22.635614

output_49_2


(4) ElasticNet

1
2
3
4
elasticnet = ElasticNet(alpha=0.5, l1_ratio=0.2)
elasticnet.fit(x_train, y_train)
elas_pred = elasticnet.predict(x_test)
mse_eval('ElasticNet(l1_ratio=0.2)', y_test, elas_pred)

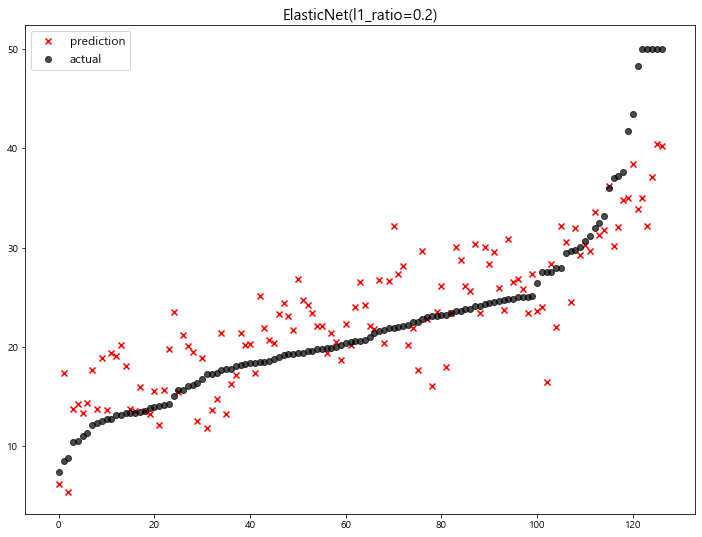
output_52_0

                      model        mse
0  ElasticNet(l1_ratio=0.2)  24.481069
1          LinearRegression  22.770784
2            Ridge(alpha=1)  22.690411
3         Lasso(alpha=0.01)  22.635614

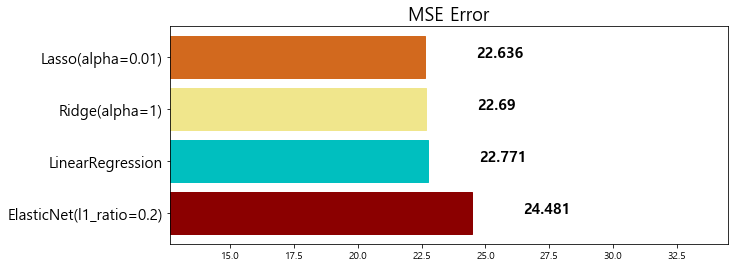
output_52_2


(5) With Standard Scaling

1
2
3
4
5
6
7
standard_elasticnet = make_pipeline(
    StandardScaler(),
    ElasticNet(alpha=0.5, l1_ratio=0.2)
)

elas_scaled_pred = standard_elasticnet.fit(x_train, y_train).predict(x_test)
mse_eval('Standard ElasticNet', y_test, elas_scaled_pred)

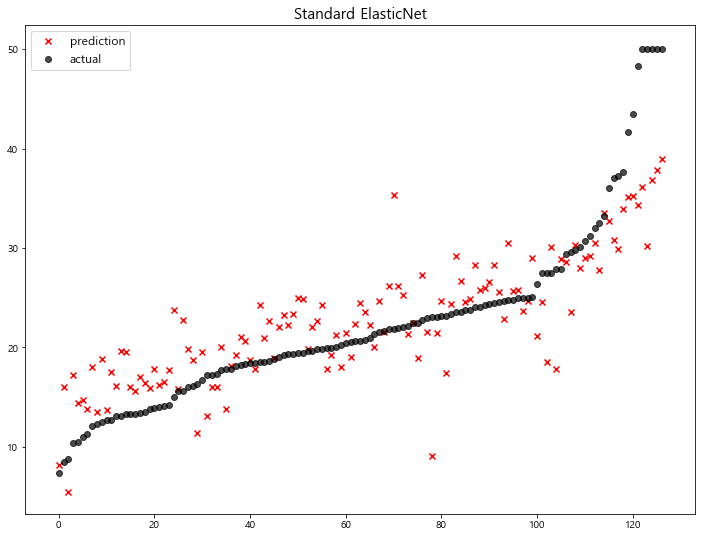
output_55_0

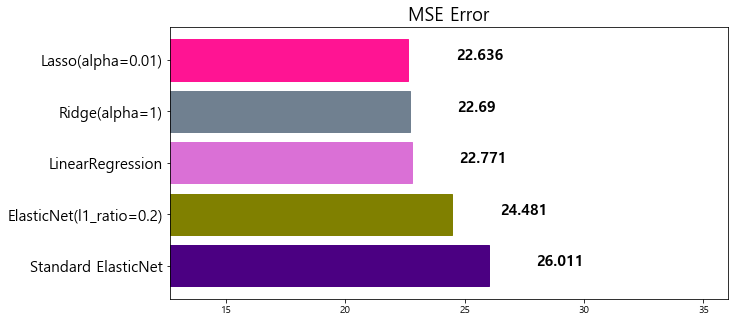
                      model        mse
0       Standard ElasticNet  26.010756
1  ElasticNet(l1_ratio=0.2)  24.481069
2          LinearRegression  22.770784
3            Ridge(alpha=1)  22.690411
4         Lasso(alpha=0.01)  22.635614

output_55_2


(6) Polynomial Features

1
2
3
4
5
6
7
8
9
# 2-Degree Polynomial Features + Standard Scaling
poly_elasticnet = make_pipeline(
    PolynomialFeatures(degree=2, include_bias=False),
    StandardScaler(),
    ElasticNet(alpha=0.5, l1_ratio=0.2)
)

poly_pred = poly_elasticnet.fit(x_train, y_train).predict(x_test)
mse_eval('Poly ElasticNet', y_test, poly_pred)

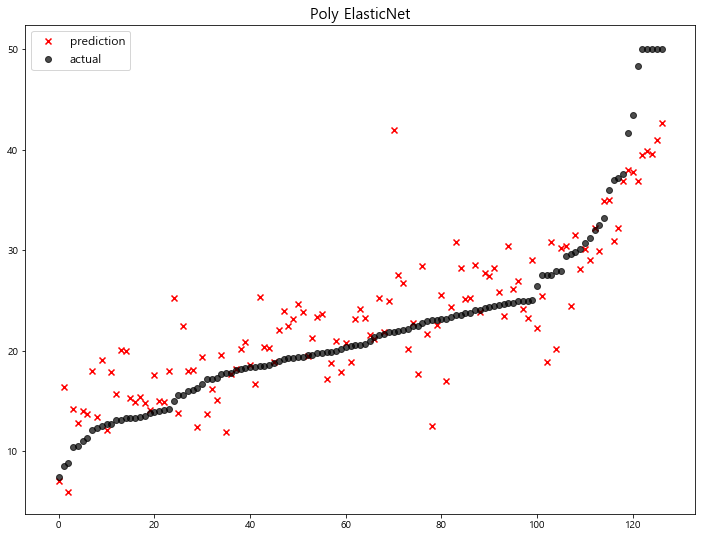
output_58_0

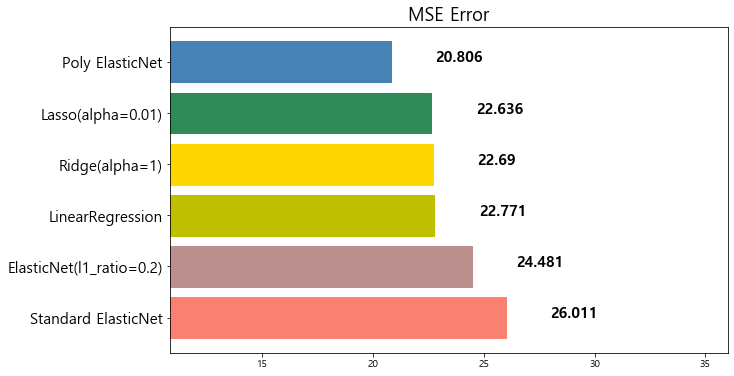
                      model        mse
0       Standard ElasticNet  26.010756
1  ElasticNet(l1_ratio=0.2)  24.481069
2          LinearRegression  22.770784
3            Ridge(alpha=1)  22.690411
4         Lasso(alpha=0.01)  22.635614
5           Poly ElasticNet  20.805986

output_58_2



4. 앙상블 (Ensemble) 알고리즘

[sklearn.ensemble] Document

앙상블 기법의 종류

  • 보팅 (Voting): 투표를 통해 결과 도출

  • 배깅 (Bagging): 샘플 중복 생성을 통해 결과 도출

  • 부스팅 (Boosting): 이전 오차를 보완하면서 가중치 부여

  • 스태킹 (Stacking): 여러 모델을 기반으로 예측된 결과를 통해 meta 모델이 다시 한번 예측


4-1. 보팅 (Voting)

>> 회귀 (Regression)

Voting은 단어 뜻 그대로 투표를 통해 최종 결과를 결정하는 방식이다. Voting과 Bagging은 모두 투표방식이지만, 다음과 같은 큰 차이점이 있다:

  • Voting은 다른 알고리즘 model을 조합해서 사용함
  • Bagging은 같은 알고리즘 내에서 다른 sample 조합을 사용함

1
from sklearn.ensemble import VotingRegressor

반드시, Tuple 형태로 모델을 정의해야 한다.

1
2
3
4
5
6
7
8
9
# 보팅에 참여한 single models 지정
single_models = [
    ('linear_reg', linear_reg),
    ('ridge', ridge),
    ('lasso', lasso),
    ('elasticnet', elasticnet),
    ('standard_elasticnet', standard_elasticnet),
    ('poly_elasticnet', poly_elasticnet)
]
1
2
# voting regressor 만들기
voting_regressor = VotingRegressor(single_models, n_jobs=-1)
1
voting_regressor.fit(x_train, y_train)
VotingRegressor(estimators=[('linear_reg',
                             LinearRegression(copy_X=True, fit_intercept=True,
                                              n_jobs=-1, normalize=False)),
                            ('ridge',
                             Ridge(alpha=1, copy_X=True, fit_intercept=True,
                                   max_iter=None, normalize=False,
                                   random_state=None, solver='auto',
                                   tol=0.001)),
                            ('lasso',
                             Lasso(alpha=0.01, copy_X=True, fit_intercept=True,
                                   max_iter=1000, normalize=False,
                                   positive=False, pr...
                                                                 interaction_only=False,
                                                                 order='C')),
                                             ('standardscaler',
                                              StandardScaler(copy=True,
                                                             with_mean=True,
                                                             with_std=True)),
                                             ('elasticnet',
                                              ElasticNet(alpha=0.5, copy_X=True,
                                                         fit_intercept=True,
                                                         l1_ratio=0.2,
                                                         max_iter=1000,
                                                         normalize=False,
                                                         positive=False,
                                                         precompute=False,
                                                         random_state=None,
                                                         selection='cyclic',
                                                         tol=0.0001,
                                                         warm_start=False))],
                                      verbose=False))],
                n_jobs=-1, weights=None)

1
2
voting_pred = voting_regressor.predict(x_test)
mse_eval('Voting Ensemble', y_test, voting_pred)

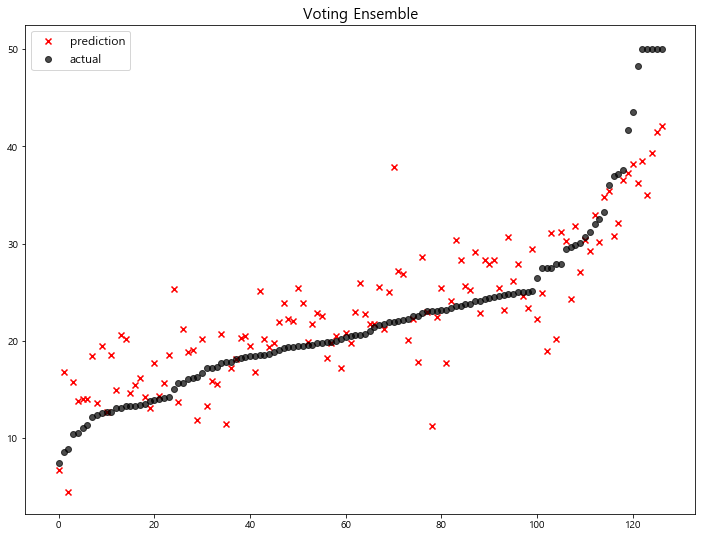
output_74_0

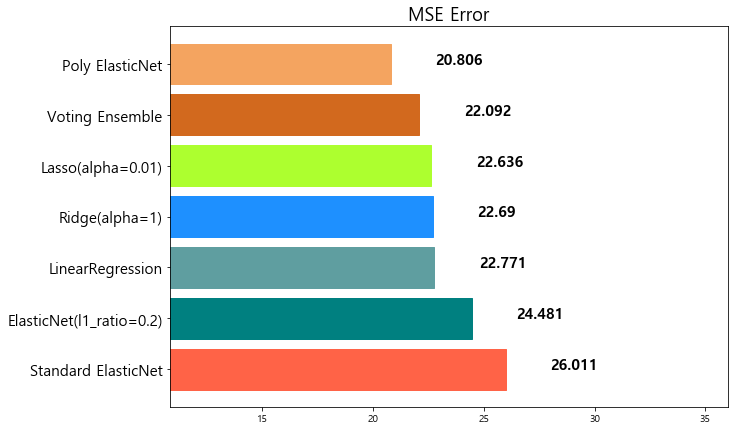
                      model        mse
0       Standard ElasticNet  26.010756
1  ElasticNet(l1_ratio=0.2)  24.481069
2          LinearRegression  22.770784
3            Ridge(alpha=1)  22.690411
4         Lasso(alpha=0.01)  22.635614
5           Voting Ensemble  22.092158
6           Poly ElasticNet  20.805986

output_74_2


>> 분류 (Classification)

참고 자료 (Blog)

분류기 모델을 만들때, Voting 앙상블은 1가지의 중요한 parameter가 있다:

  • voting = {‘hard’, ‘soft’}

class를 0, 1로 분류 예측을 하는 이진 분류를 예로 들어 보자.

(1) hard 로 설정한 경우

Hard Voting 방식에서는 결과 값에 대한 다수 class를 사용한다.

분류를 예측한 값이 1, 0, 0, 1, 1 이었다고 가정한다면 1이 3표, 0이 2표를 받았기 때문에 Hard Voting 방식에서는 1이 최종 값으로 예측을 하게 된다.


(2) soft 로 설정한 경우

soft voting 방식은 각각의 확률의 평균 값을 계산한다음에 가장 확률이 높은 값으로 확정짓게 된다.

가령 class 0이 나올 확률이 (0.4, 0.9, 0.9, 0.4, 0.4)이었고, class 1이 나올 확률이 (0.6, 0.1, 0.1, 0.6, 0.6) 이었다면,

  • class 0이 나올 최종 확률은 (0.4+0.9+0.9+0.4+0.4) / 5 = 0.44,
  • class 1이 나올 최종 확률은 (0.6+0.1+0.1+0.6+0.6) / 5 = 0.4

가 되기 때문에 앞선 Hard Voting의 결과와는 다른 결과 값이 최종으로 선출되게 된다.


1
2
from sklearn.ensemble import VotingClassifier
from sklearn.linear_model import LogisticRegression, RidgeClassifier
1
2
3
4
models = [
    ('Logit', LogisticRegression()),
    ('ridge', RidgeClassifier())
]

voting 옵션 지정

1
vc = VotingClassifier(models, voting='soft')

4-2. 배깅 (Bagging)

참고 자료 (Blog)

Bagging은 Bootstrap Aggregating의 줄임말이다.

Bootstrap은 여러 개의 dataset을 중첩을 허용하게 하여 샘플링하여 분할하는 방식.

데이터 셋의 구성이 [1, 2, 3, 4, 5]로 되어 있다면,

  1. group 1 = [1, 2, 3]
  2. group 2 = [1, 3, 4]
  3. group 3 = [2, 3, 5]
1
Image('https://teddylee777.github.io/images/2019-12-17/image-20191217015537872.png')

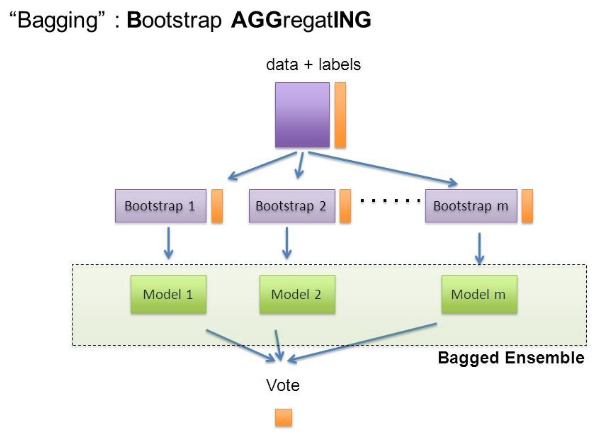
output_94_0


Voting VS Bagging

  • Voting은 여러 알고리즘의 조합에 대한 앙상블
  • Bagging은 하나의 단일 알고리즘에 대하여 여러 개의 샘플 조합으로 앙상블

대표적인 Bagging 앙상블

  1. Random Forest

  2. Bagging


>> Random Forest

  • Decision Tree 기반 Bagging 앙상블
  • 굉장히 인기있는 앙상블 모델
  • 사용성이 쉽고, 성능도 우수함

[sklearn.ensemble.RandomForestRegressor] Document
[sklearn.ensemble.RandomForestClassifier] Document


  • 회귀 (Regression)

Hyper-parameter의 default value로 모델 학습

1
from sklearn.ensemble import RandomForestRegressor
1
2
rfr = RandomForestRegressor(random_state=1)
rfr.fit(x_train, y_train)
RandomForestRegressor(bootstrap=True, ccp_alpha=0.0, criterion='mse',
                      max_depth=None, max_features='auto', max_leaf_nodes=None,
                      max_samples=None, min_impurity_decrease=0.0,
                      min_impurity_split=None, min_samples_leaf=1,
                      min_samples_split=2, min_weight_fraction_leaf=0.0,
                      n_estimators=100, n_jobs=None, oob_score=False,
                      random_state=1, verbose=0, warm_start=False)

1
2
rfr_pred = rfr.predict(x_test)
mse_eval('RandomForest Ensemble', y_test, rfr_pred)

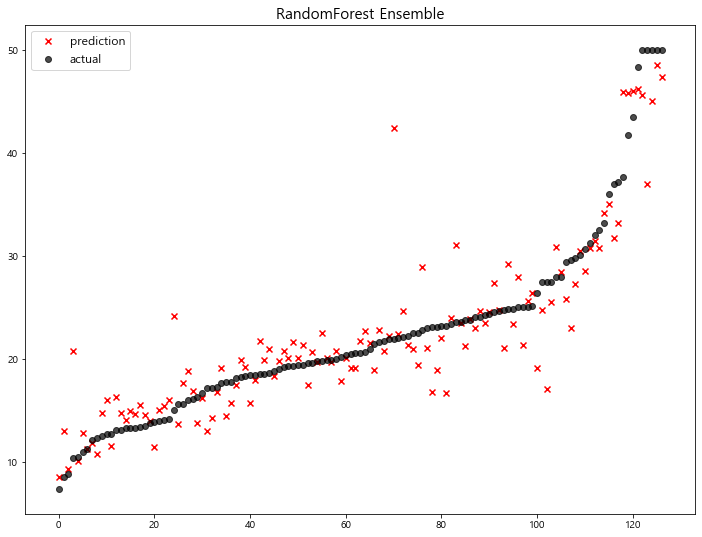
output_107_0

                      model        mse
0       Standard ElasticNet  26.010756
1  ElasticNet(l1_ratio=0.2)  24.481069
2          LinearRegression  22.770784
3            Ridge(alpha=1)  22.690411
4         Lasso(alpha=0.01)  22.635614
5           Voting Ensemble  22.092158
6           Poly ElasticNet  20.805986
7     RandomForest Ensemble  13.781191

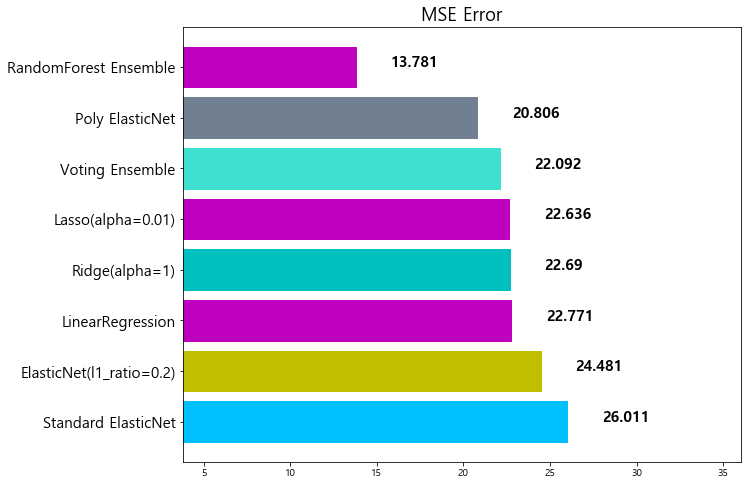
output_107_2


주요 Hyper-parameter

  • random_state: random seed 고정 값
  • n_jobs: CPU 사용 갯수
  • max_depth: 깊어질 수 있는 최대 깊이. 과대적합 방지용
  • n_estimators: 암상블하는 트리의 갯수
  • max_features: best split을 판단할 때 최대로 사용할 feature의 갯수 {‘auto’, ‘sqrt’, ‘log2’}. 과대적합 방지용
  • min_samples_split: 트리가 분할할 때 최소 샘플의 갯수. default=2. 과대적합 방지용
1
Image('https://teddylee777.github.io/images/2020-01-09/decistion-tree.png', width=600)
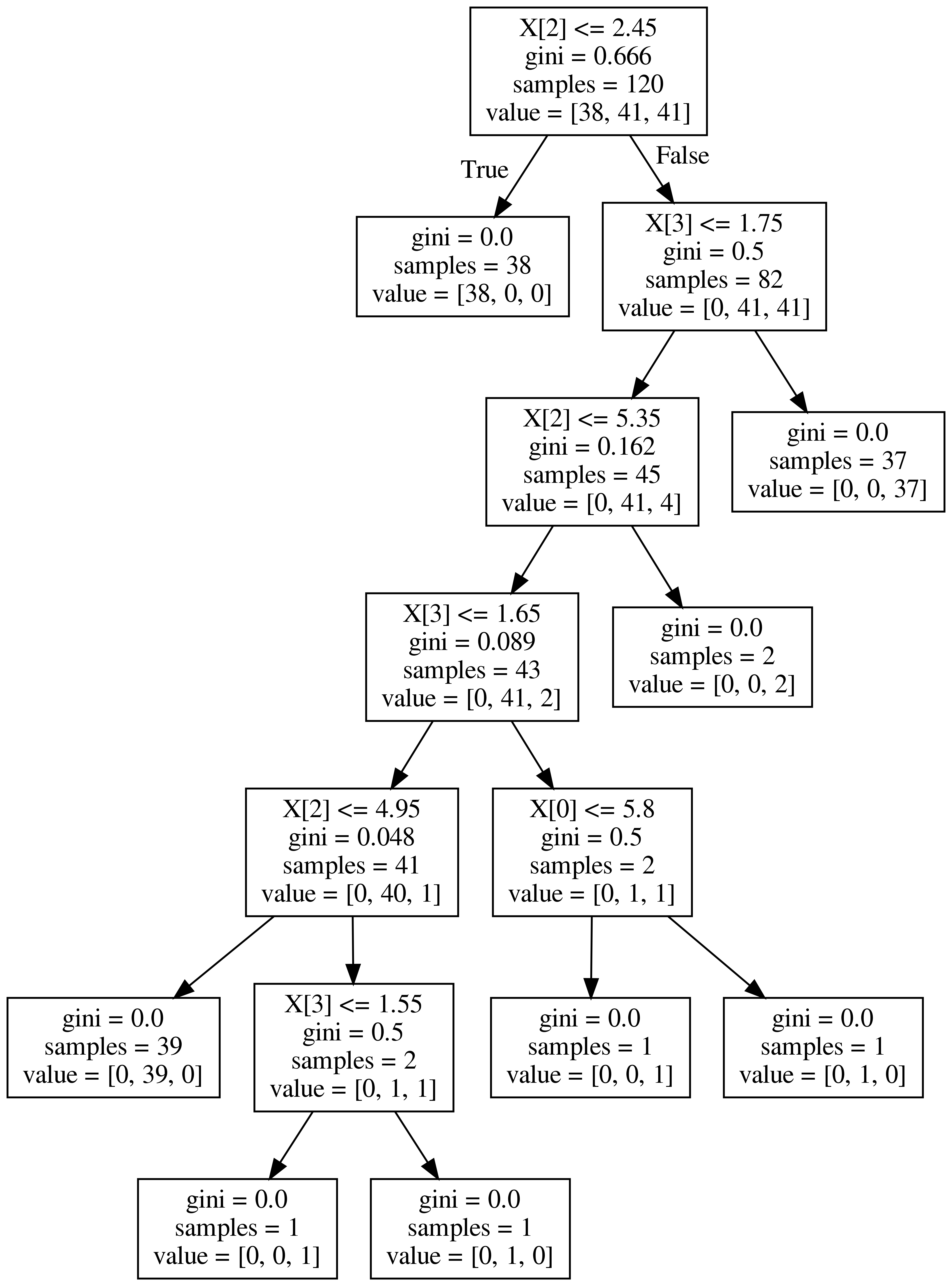
output_110_0

With Hyper-parameter Tuning

1
2
3
4
rfr_t = RandomForestRegressor(random_state=1, n_estimators=500, max_depth=7, max_features='sqrt')
rfr_t.fit(x_train, y_train)
rfr_t_pred = rfr_t.predict(x_test)
mse_eval('RandomForest Ensemble w/ Tuning', y_test, rfr_t_pred)

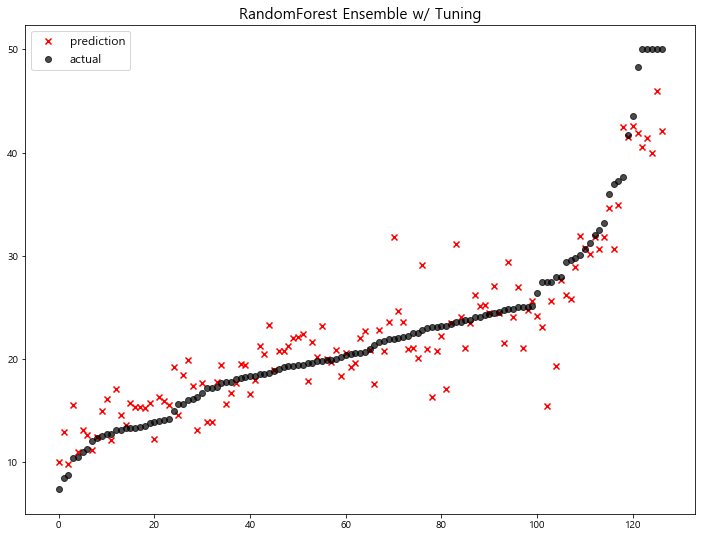
output_113_0

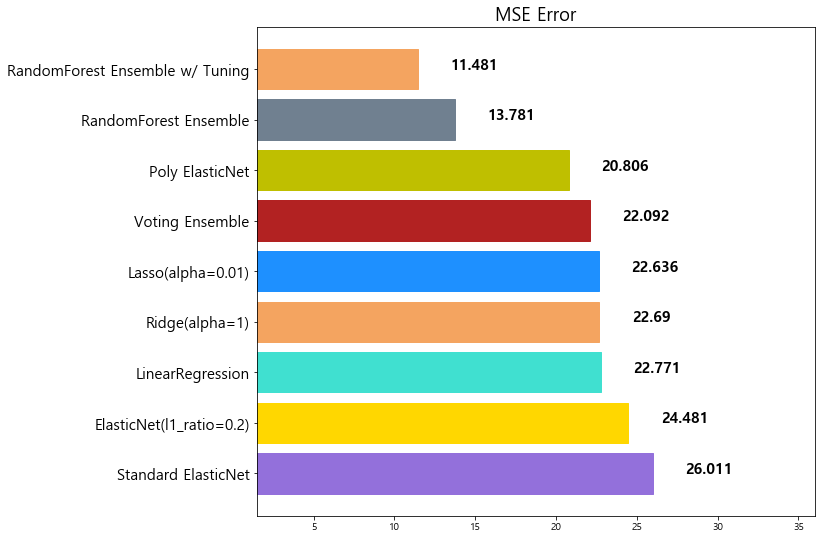
                             model        mse
0              Standard ElasticNet  26.010756
1         ElasticNet(l1_ratio=0.2)  24.481069
2                 LinearRegression  22.770784
3                   Ridge(alpha=1)  22.690411
4                Lasso(alpha=0.01)  22.635614
5                  Voting Ensemble  22.092158
6                  Poly ElasticNet  20.805986
7            RandomForest Ensemble  13.781191
8  RandomForest Ensemble w/ Tuning  11.481491

output_113_2


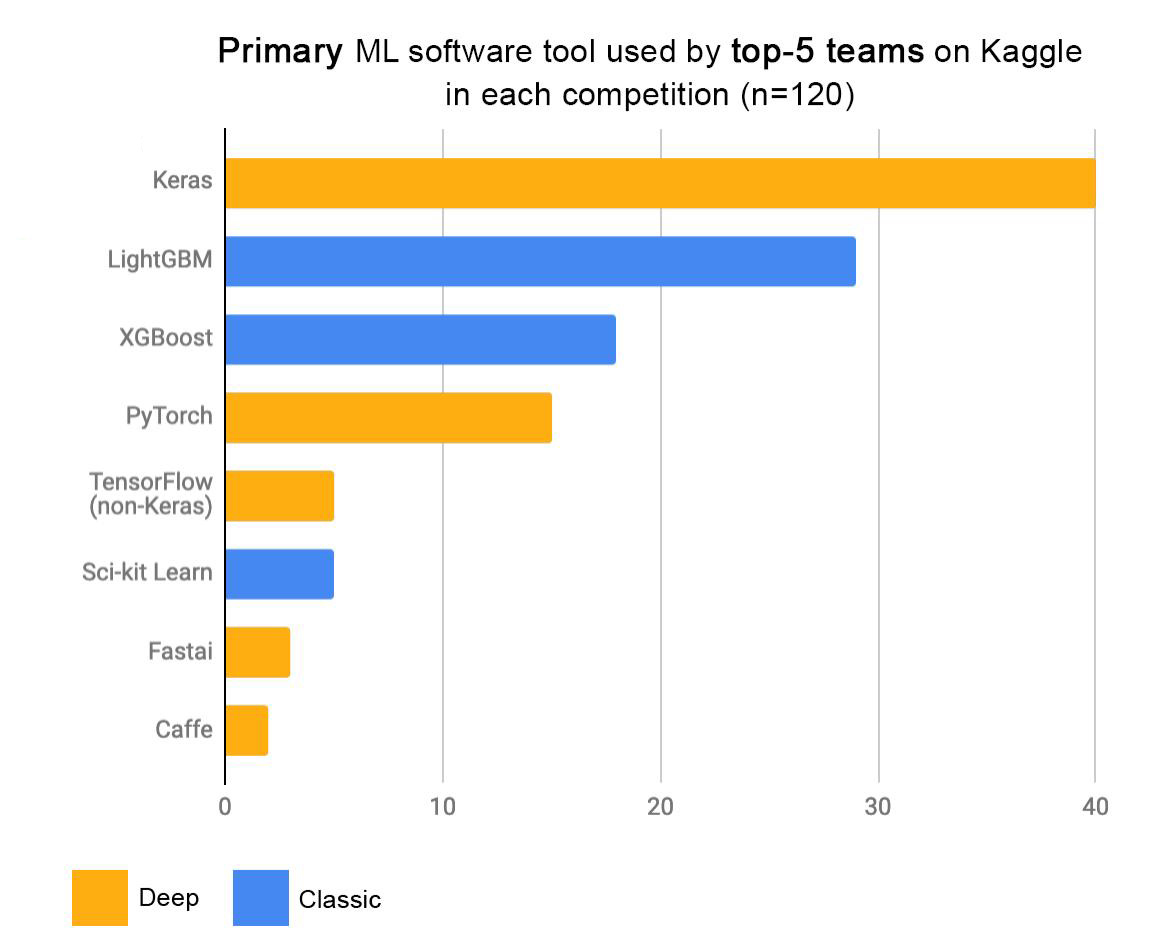
4-3. 부스팅 (Boosting)

참고 자료 (Blog)

악한 학습기를 순차적으로 학습을 하되, 이전 학습에 대하여 잘멋 예측된 데이터에 가중치를 부여해 오차를 보완해 나가는 방식이다.

장점

  • 성능이 매우 우수하다 (LightGBM, XGBoost)

단점

  • 부스팅 알고리즘의 특성상 계속 약점(오분류/잔차)을 보완하려고 하기 때문에 잘못된 레이블링이나 아웃라이어에 필요 이상으로 민감할 수 있다
  • 다른 앙상블 대비 학습 시간이 오래걸린다는 단점이 존재
1
Image('https://keras.io/img/graph-kaggle-1.jpeg', width=800)

output_120_0


대표적인 Boosting 앙상블

  1. AdaBoost

  2. GradientBoost

  3. LightGBM (LGBM)

  4. XGBoost


4-3-1. Gradient Boost

  • 장점: 성능이 우수함
  • 단점: 학습 시간이 너무 오래 걸린다

[sklearn.ensemble.GradientBoostingRegressor] Document

1
from sklearn.ensemble import GradientBoostingRegressor, GradientBoostingClassifier
1
2
3
# default value로 학습
gbr = GradientBoostingRegressor(random_state=1)
gbr.fit(x_train, y_train)
GradientBoostingRegressor(alpha=0.9, ccp_alpha=0.0, criterion='friedman_mse',
                          init=None, learning_rate=0.1, loss='ls', max_depth=3,
                          max_features=None, max_leaf_nodes=None,
                          min_impurity_decrease=0.0, min_impurity_split=None,
                          min_samples_leaf=1, min_samples_split=2,
                          min_weight_fraction_leaf=0.0, n_estimators=100,
                          n_iter_no_change=None, presort='deprecated',
                          random_state=1, subsample=1.0, tol=0.0001,
                          validation_fraction=0.1, verbose=0, warm_start=False)

1
2
gbr_pred = gbr.predict(x_test)
mse_eval('GradientBoost Ensemble', y_test, gbr_pred)

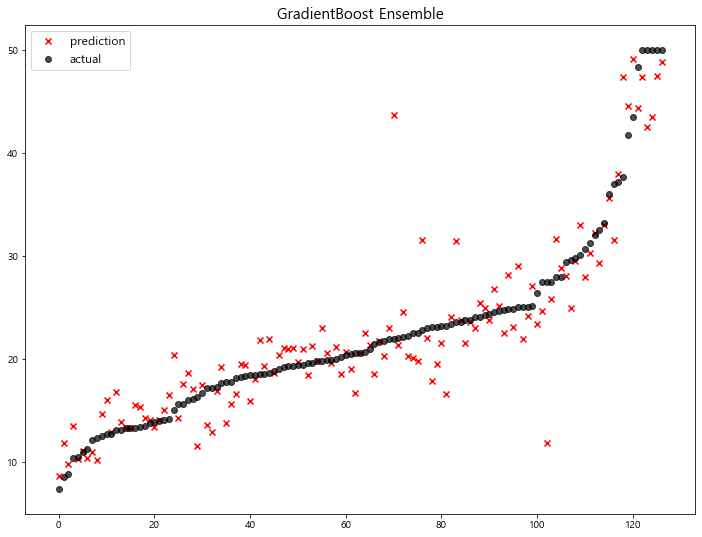
output_129_0

                             model        mse
0              Standard ElasticNet  26.010756
1         ElasticNet(l1_ratio=0.2)  24.481069
2                 LinearRegression  22.770784
3                   Ridge(alpha=1)  22.690411
4                Lasso(alpha=0.01)  22.635614
5                  Voting Ensemble  22.092158
6                  Poly ElasticNet  20.805986
7            RandomForest Ensemble  13.781191
8           GradientBoost Ensemble  13.451877
9  RandomForest Ensemble w/ Tuning  11.481491

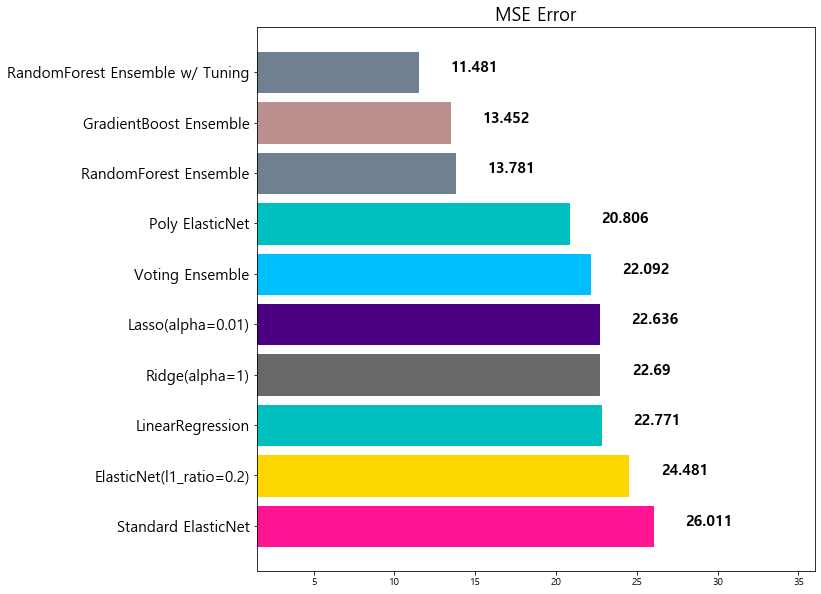
output_129_2


주요 Hyper-parameter

  • random_state: random seed 고정 값
  • n_jobs: CPU 사용 갯수
  • learning rate: 학습율. 너무 큰 학습율은 성능을 떨어뜨리고, 너무 작은 학습율은 학습이 느리다. 적절한 값을 찾아야함. default=0.1 (n_estimators와 같이 튜닝해야 함)
  • n_estimators: 부스팅 스테이지 수. default=100
    (Random Forest 트리의 갯수 설정과 비슷)
  • subsample: 샘플 사용 비율 (max_features와 비슷). 과대적합 방지용
  • min_samples_split: 노드 분할시 최소 샘플의 갯수. default=2. 과대적합 방지용

There’s a trade-off between learning_rate and n_estimators.
둘의 곱을 유지하는 것이 좋다


1
2
3
4
5
6
# with hyper-parameter tuning
# learning_rate=0.01 (without tuning n_estimators together)
gbr_t = GradientBoostingRegressor(random_state=1, learning_rate=0.01)
gbr_t.fit(x_train, y_train)
gbr_t_pred = gbr_t.predict(x_test)
mse_eval('GradientBoost Ensemble w/ tuning (lr=0.01)', y_test, gbr_t_pred)

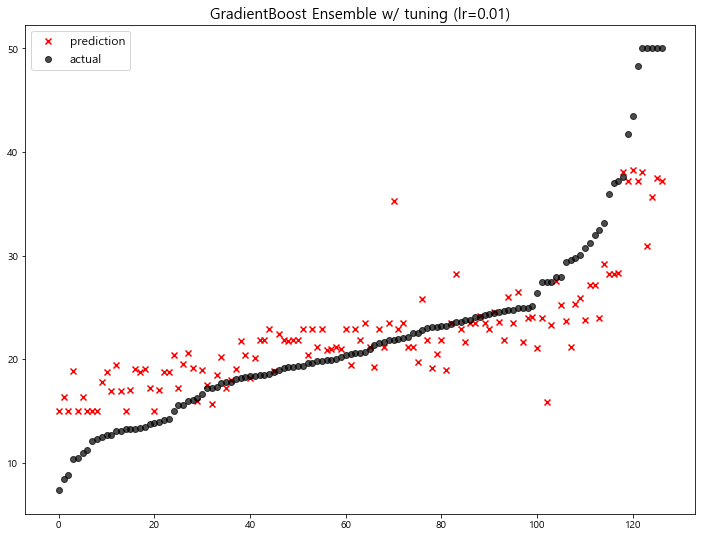
output_133_0

                                         model        mse
0                          Standard ElasticNet  26.010756
1   GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                     ElasticNet(l1_ratio=0.2)  24.481069
3                             LinearRegression  22.770784
4                               Ridge(alpha=1)  22.690411
5                            Lasso(alpha=0.01)  22.635614
6                              Voting Ensemble  22.092158
7                              Poly ElasticNet  20.805986
8                        RandomForest Ensemble  13.781191
9                       GradientBoost Ensemble  13.451877
10             RandomForest Ensemble w/ Tuning  11.481491

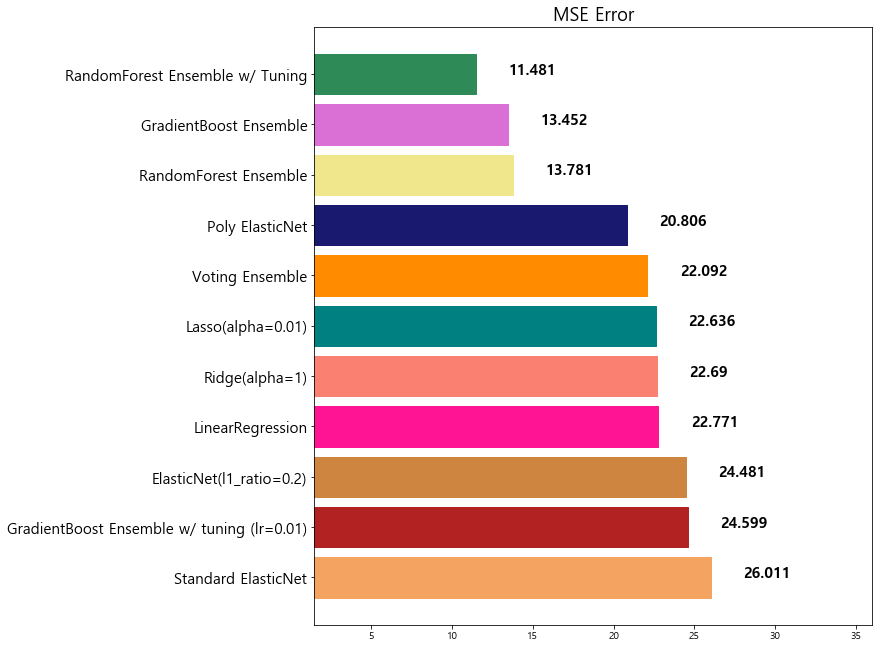
output_133_2


1
2
3
4
5
# tuning: learning_rate=0.01, n_estimators=1000
gbr_t2 = GradientBoostingRegressor(random_state=1, learning_rate=0.01, n_estimators=1000)
gbr_t2.fit(x_train, y_train)
gbr_t2_pred = gbr_t2.predict(x_test)
mse_eval('GradientBoost Ensemble w/ tuning (lr=0.01, est=1000)', y_test, gbr_t2_pred)

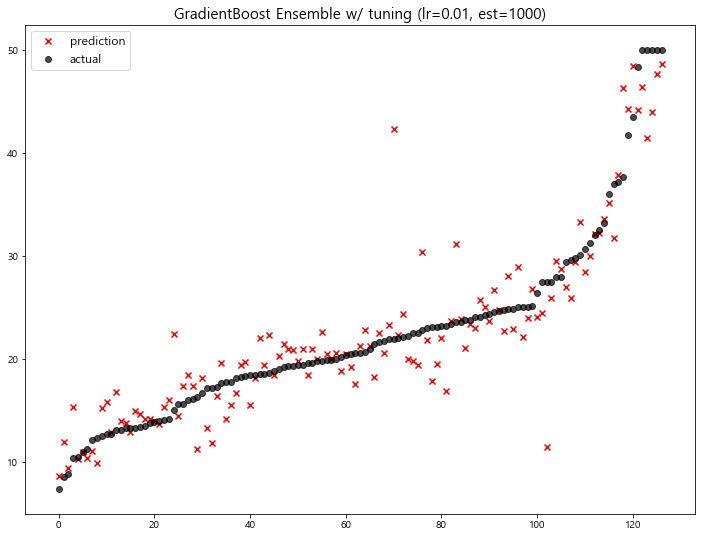
output_135_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                               RandomForest Ensemble  13.781191
9                              GradientBoost Ensemble  13.451877
10  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
11                    RandomForest Ensemble w/ Tuning  11.481491

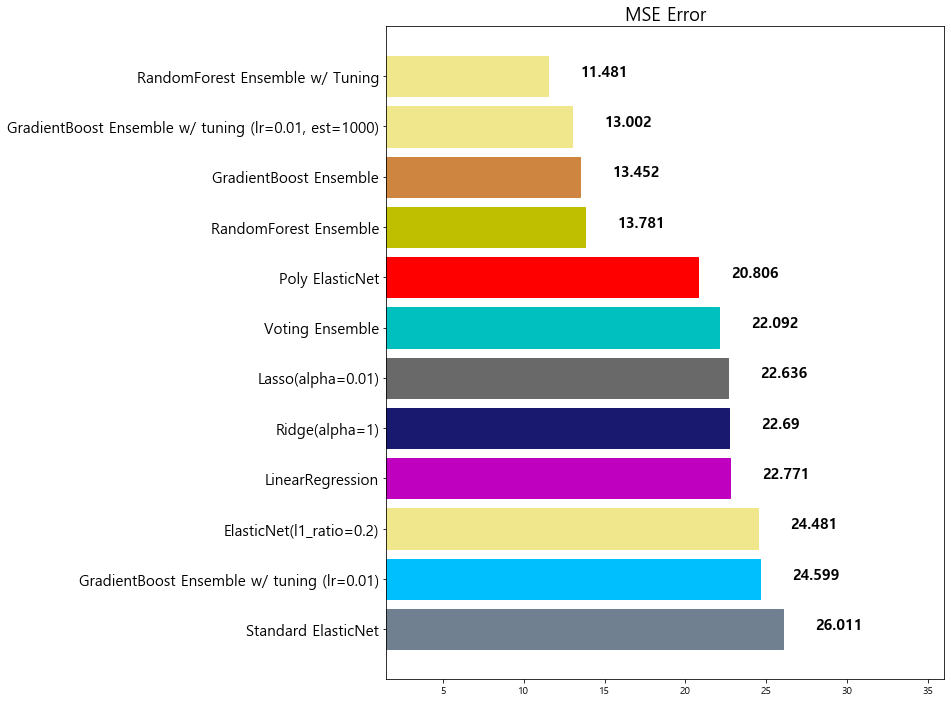
output_135_2


1
2
3
4
5
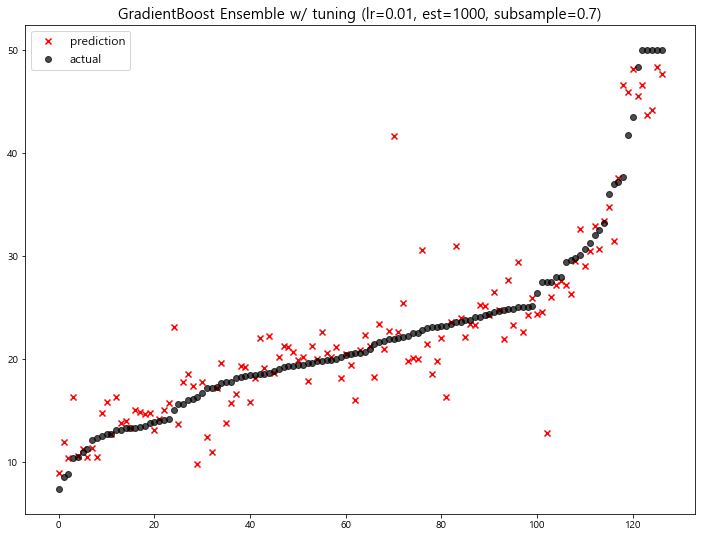
# tuning: learning_rate=0.01, n_estimators=1000, subsample=0.8
gbr_t3 = GradientBoostingRegressor(random_state=42, learning_rate=0.01, n_estimators=1000, subsample=0.7)
gbr_t3.fit(x_train, y_train)
gbr_t3_pred = gbr_t3.predict(x_test)
mse_eval('GradientBoost Ensemble w/ tuning (lr=0.01, est=1000, subsample=0.7)', y_test, gbr_t3_pred)

output_137_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                               RandomForest Ensemble  13.781191
9                              GradientBoost Ensemble  13.451877
10  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
11  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
12                    RandomForest Ensemble w/ Tuning  11.481491

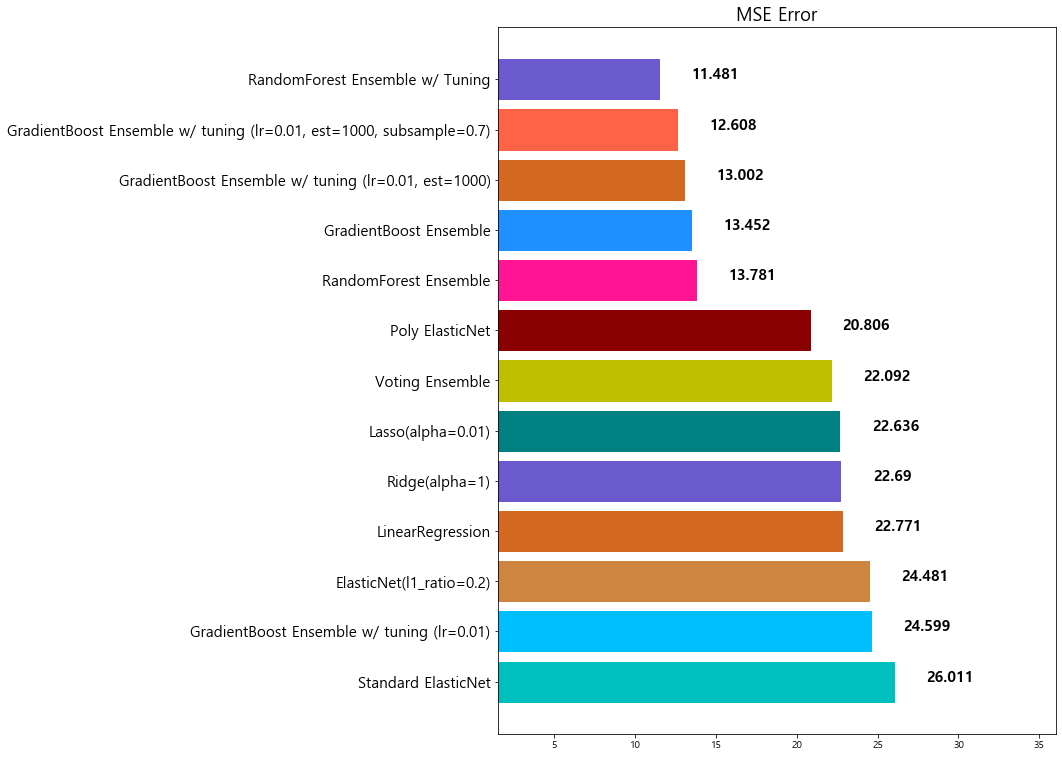
output_137_2


4-3-2. XGBoost

eXtreme Gradient Boosting

[XGBoost] Document

주요 특징

  • scikit-learn 패키지 아님

  • 성능이 우수함

  • GBM보다는 빠르고 성능도 향상됨

  • 여전히 학습 속도가 느림


1
pip install xgboost
Requirement already satisfied: xgboost in d:\anaconda\lib\site-packages (1.1.1)
Requirement already satisfied: scipy in d:\anaconda\lib\site-packages (from xgboost) (1.4.1)
Requirement already satisfied: numpy in d:\anaconda\lib\site-packages (from xgboost) (1.18.1)
Note: you may need to restart the kernel to use updated packages.

1
from xgboost import XGBRegressor, XGBClassifier
1
2
3
# default value로 학습
xgb = XGBRegressor(random_state=1)
xgb.fit(x_train, y_train)
XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=1,
             colsample_bynode=1, colsample_bytree=1, gamma=0, gpu_id=-1,
             importance_type='gain', interaction_constraints='',
             learning_rate=0.300000012, max_delta_step=0, max_depth=6,
             min_child_weight=1, missing=nan, monotone_constraints='()',
             n_estimators=100, n_jobs=0, num_parallel_tree=1,
             objective='reg:squarederror', random_state=1, reg_alpha=0,
             reg_lambda=1, scale_pos_weight=1, subsample=1, tree_method='exact',
             validate_parameters=1, verbosity=None)

1
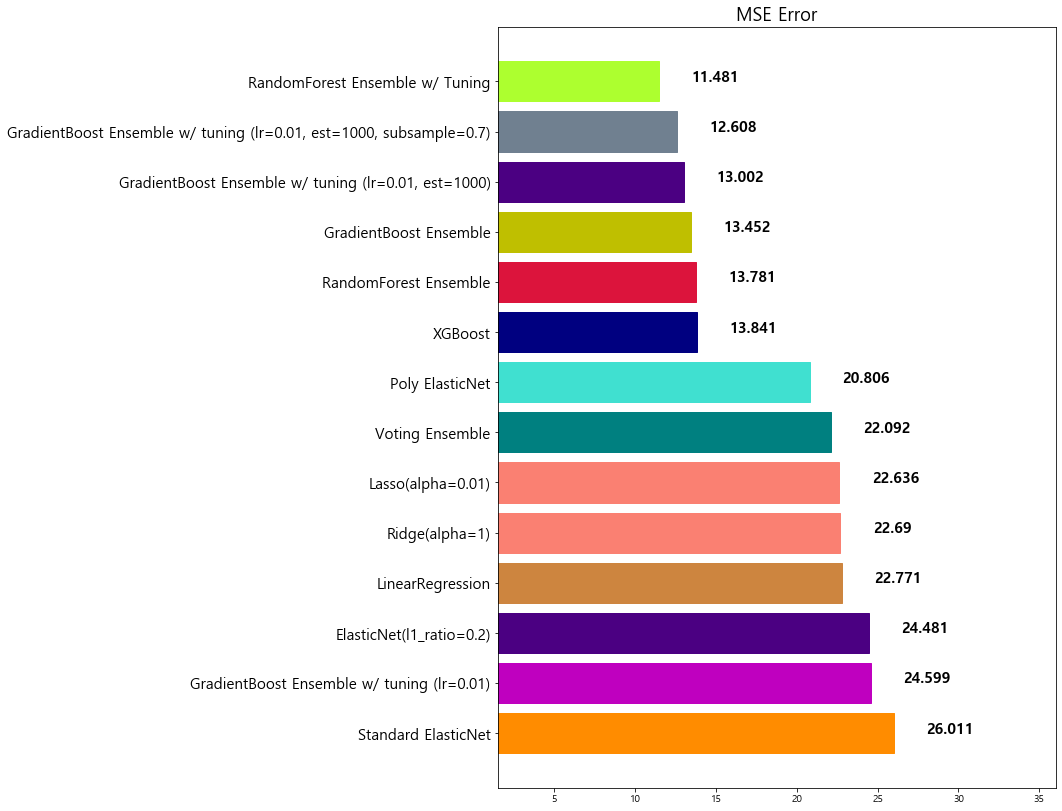
2
xgb_pred = xgb.predict(x_test)
mse_eval('XGBoost', y_test, xgb_pred)

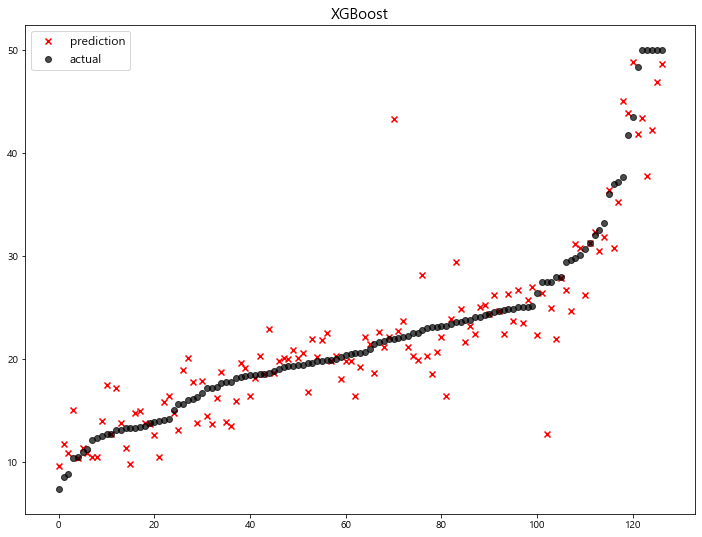
output_146_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                             XGBoost  13.841454
9                               RandomForest Ensemble  13.781191
10                             GradientBoost Ensemble  13.451877
11  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
13                    RandomForest Ensemble w/ Tuning  11.481491

output_146_2


주요 Hyper-parameter

  • random_state: random seed 고정 값

  • n_jobs: CPU 사용 갯수

  • learning_rate: 학습율. 너무 큰 학습율은 성능을 떨어뜨리고, 너무 작은 학습율은 학습이 느리다. 적절한 값을 찾아야함. n_estimators와 같이 튜닝. default=0.1

  • n_estimators: 부스팅 스테이지 수. (랜덤포레스트 트리의 갯수 설정과 비슷한 개념). default=100

  • max_depth: 트리의 깊이. 과대적합 방지용. default=3.

  • subsample: 샘플 사용 비율. 과대적합 방지용. default=1.0

  • max_features: 최대로 사용할 feature의 비율. 과대적합 방지용. default=1.0


1
2
3
4
5
# with hyeper-parameter tuning
xgb_t = XGBRegressor(random_state=1, learning_rate=0.01, n_estimators=1000, subsample=0.7, max_features=0.8, max_depth=7)
xgb_t.fit(x_train, y_train)
xgb_t_pred = xgb_t.predict(x_test)
mse_eval('XGBoost w/ Tuning', y_test, xgb_t_pred)
[16:55:00] WARNING: C:\Users\Administrator\workspace\xgboost-win64_release_1.1.0\src\learner.cc:480: 
Parameters: { max_features } might not be used.

  This may not be accurate due to some parameters are only used in language bindings but
  passed down to XGBoost core.  Or some parameters are not used but slip through this
  verification. Please open an issue if you find above cases.

​
​

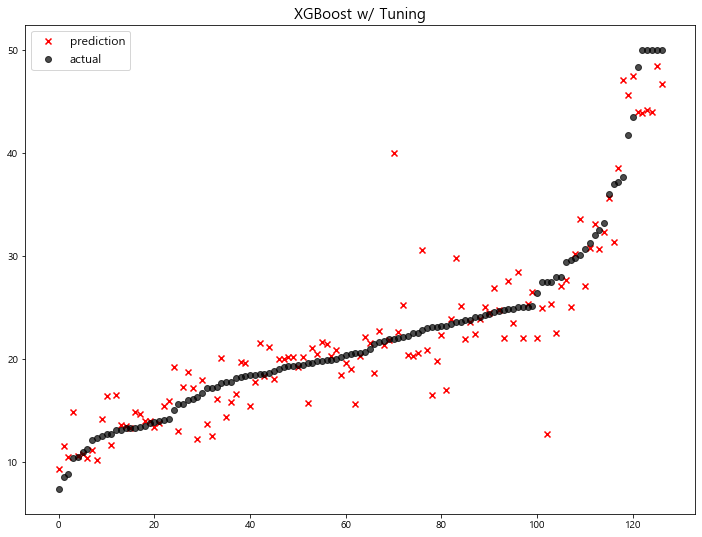
output_150_1

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                             XGBoost  13.841454
9                               RandomForest Ensemble  13.781191
10                             GradientBoost Ensemble  13.451877
11  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
13                                  XGBoost w/ Tuning  11.987602
14                    RandomForest Ensemble w/ Tuning  11.481491

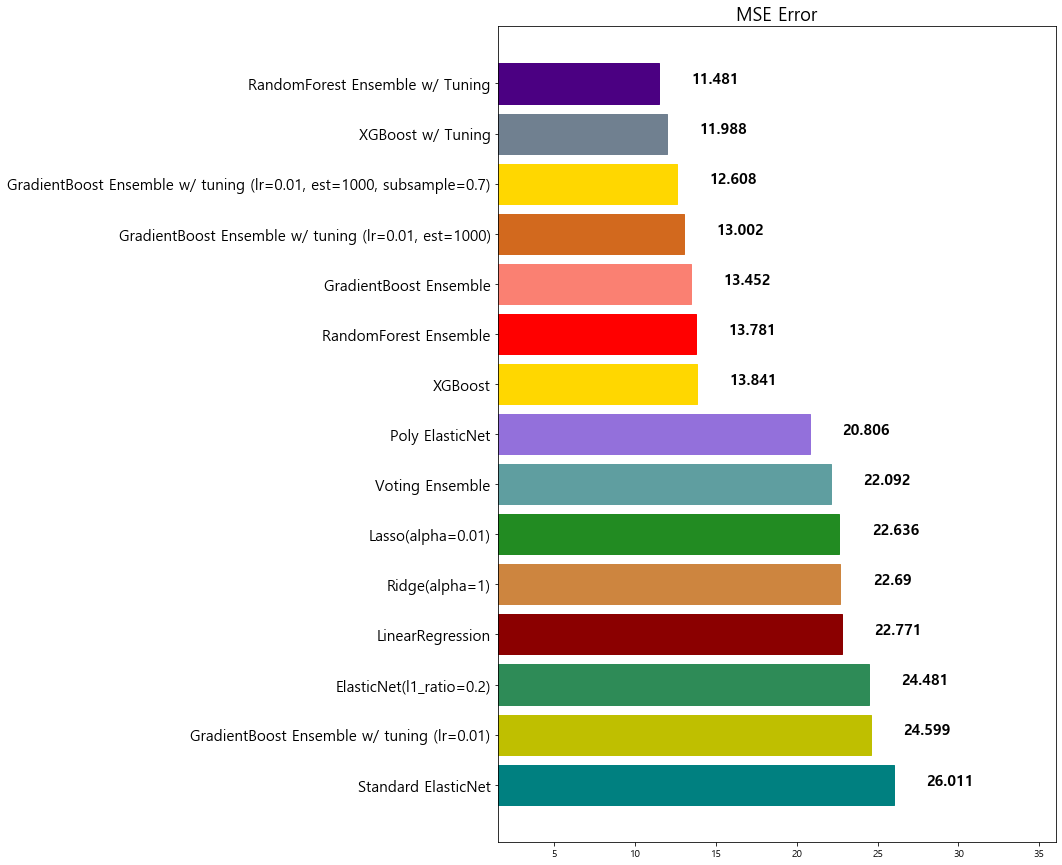
output_150_3


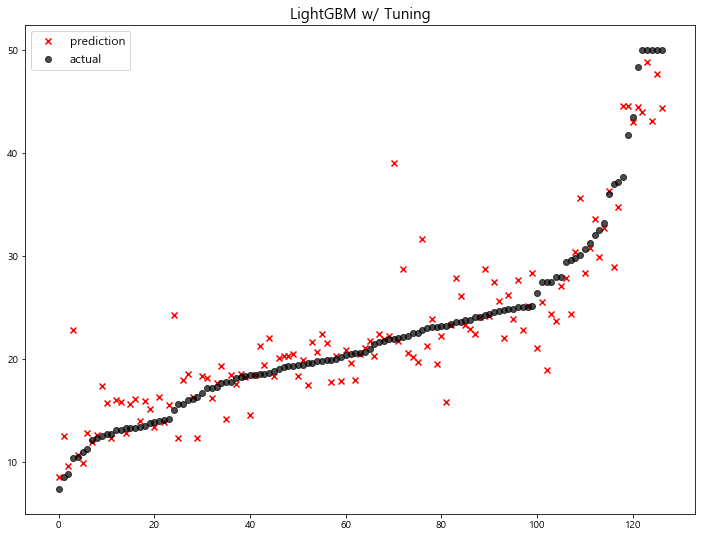
4-3-3. LightGBM

[LightGBM] Document

주요 특징

  • scikit-learn 패키지가 아님

  • 성능이 우수함

  • 속도도 매우 빠름


1
pip install lightgbm
Requirement already satisfied: lightgbm in d:\anaconda\lib\site-packages (2.3.1)
Requirement already satisfied: scipy in d:\anaconda\lib\site-packages (from lightgbm) (1.4.1)
Requirement already satisfied: numpy in d:\anaconda\lib\site-packages (from lightgbm) (1.18.1)
Requirement already satisfied: scikit-learn in d:\anaconda\lib\site-packages (from lightgbm) (0.22.1)
Requirement already satisfied: joblib>=0.11 in d:\anaconda\lib\site-packages (from scikit-learn->lightgbm) (0.14.1)
Note: you may need to restart the kernel to use updated packages.

1
from lightgbm import LGBMRegressor, LGBMClassifier
1
2
3
# default value 로 학습
lgbm = LGBMRegressor(random_state=1)
lgbm.fit(x_train, y_train)
LGBMRegressor(boosting_type='gbdt', class_weight=None, colsample_bytree=1.0,
              importance_type='split', learning_rate=0.1, max_depth=-1,
              min_child_samples=20, min_child_weight=0.001, min_split_gain=0.0,
              n_estimators=100, n_jobs=-1, num_leaves=31, objective=None,
              random_state=1, reg_alpha=0.0, reg_lambda=0.0, silent=True,
              subsample=1.0, subsample_for_bin=200000, subsample_freq=0)

1
2
lgbm_pred = lgbm.predict(x_test)
mse_eval('LightGBM', y_test, lgbm_pred)

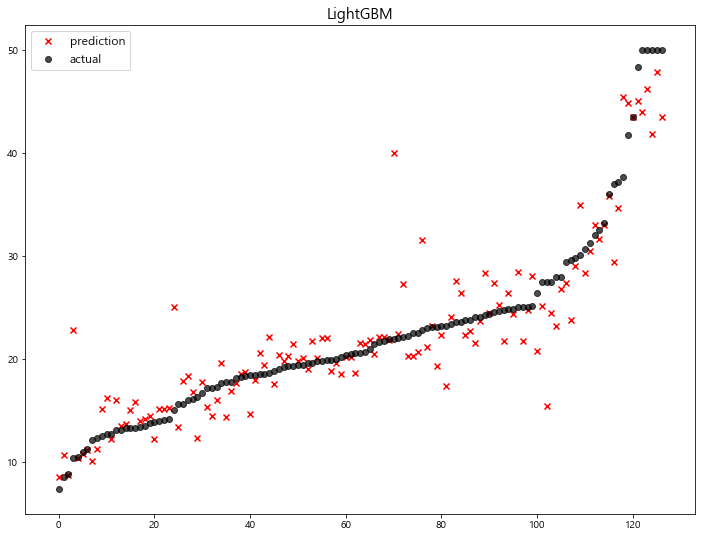
output_158_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                             XGBoost  13.841454
9                               RandomForest Ensemble  13.781191
10                             GradientBoost Ensemble  13.451877
11  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
12                                           LightGBM  12.882170
13  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
14                                  XGBoost w/ Tuning  11.987602
15                    RandomForest Ensemble w/ Tuning  11.481491

output_158_2


주요 Hyperparameter

  • random_state: random seed 고정 값

  • n_jobs: CPU 사용 갯수

  • learning_rate: 학습율. 너무 큰 학습율은 성능을 떨어뜨리고, 너무 작은 학습율은 학습이 느리다. 적절한 값을 찾아야함. n_estimators와 같이 튜닝. default=0.1

  • n_estimators: 부스팅 스테이지 수. (랜덤포레스트 트리의 갯수 설정과 비슷한 개념). default=100

  • max_depth: 트리의 깊이. 과대적합 방지용. default=3.

  • colsample_bytree: 샘플 사용 비율 (max_features와 비슷한 개념). 과대적합 방지용. default=1.0


1
2
3
4
5
# with hyper-parameter tuning
lgbm_t = LGBMRegressor(random_state=1, learning_rate=0.01, n_estimators=2000, colsample_bytree=0.9, subsample=0.7, max_depth=5)
lgbm_t.fit(x_train, y_train)
lgbm_t_pred = lgbm_t.predict(x_test)
mse_eval('LightGBM w/ Tuning', y_test, lgbm_t_pred)

output_162_0

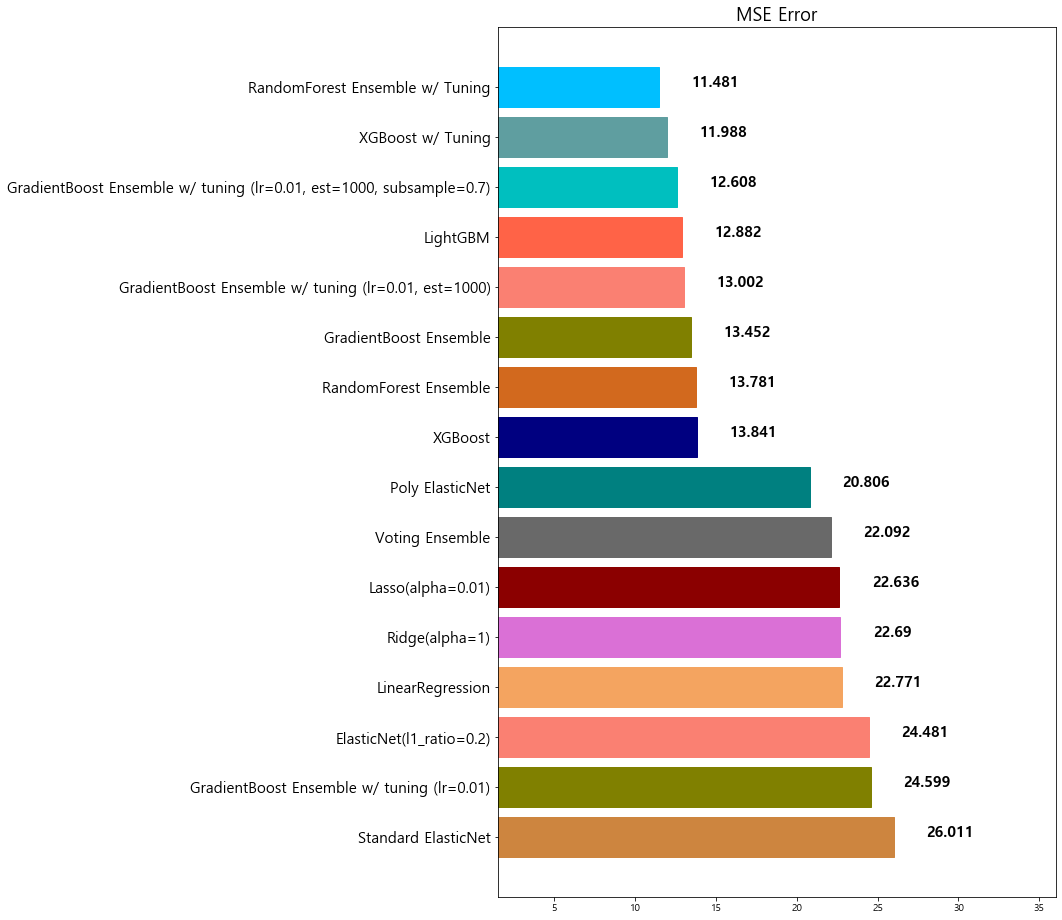
                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                             XGBoost  13.841454
9                               RandomForest Ensemble  13.781191
10                             GradientBoost Ensemble  13.451877
11  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
12                                           LightGBM  12.882170
13  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
14                                 LightGBM w/ Tuning  12.200040
15                                  XGBoost w/ Tuning  11.987602
16                    RandomForest Ensemble w/ Tuning  11.481491

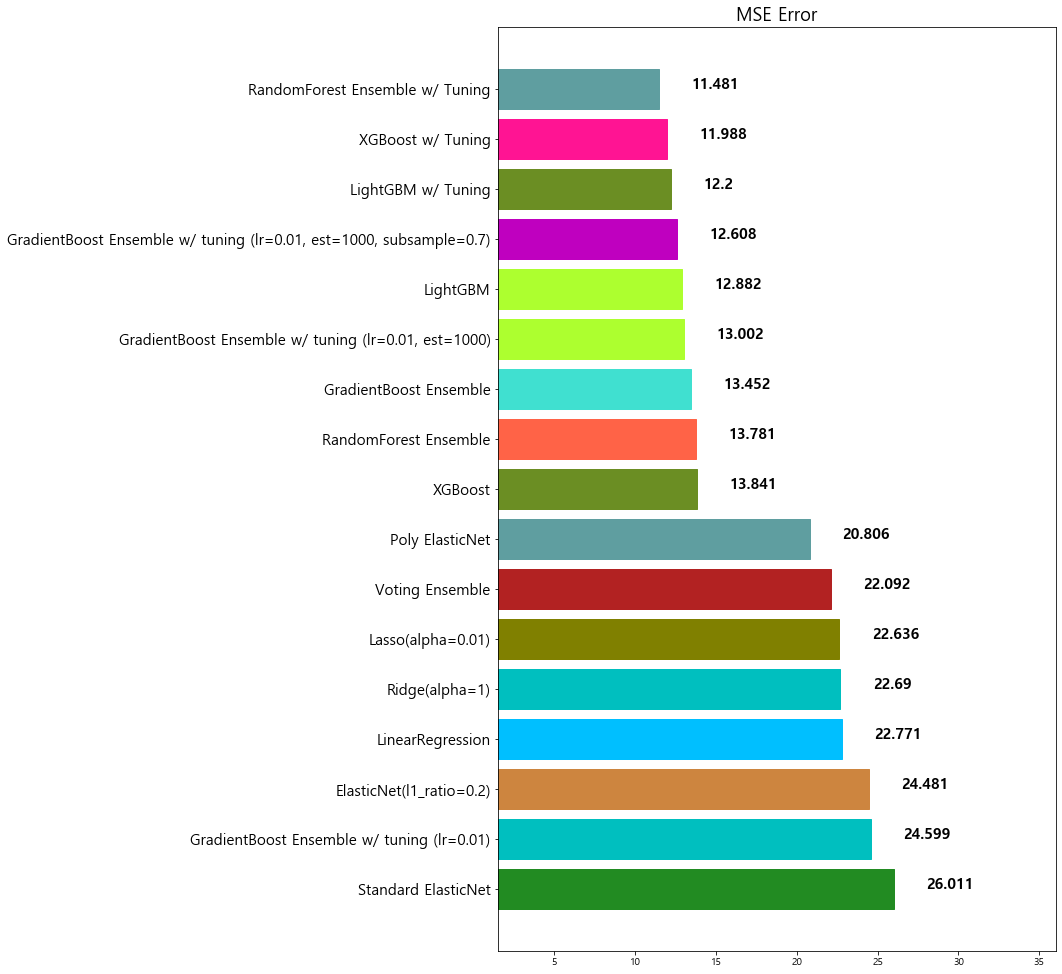
output_162_2


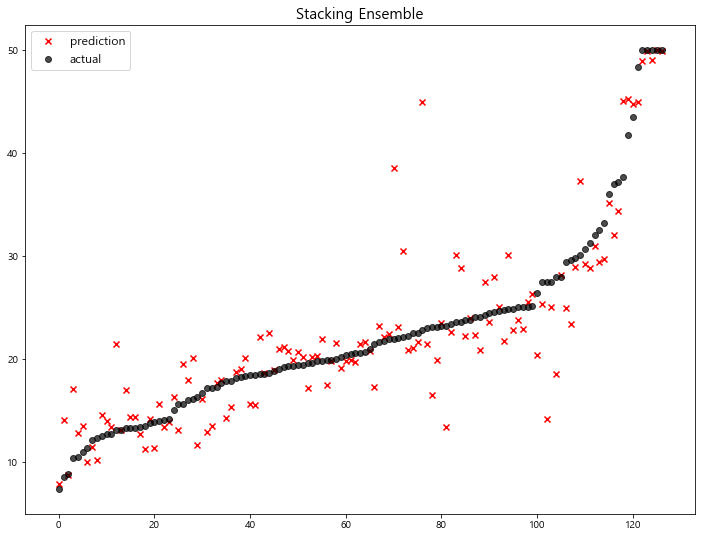
4-4. 스태킹 (Stacking)

개별 모델이 예측한 데이터를 기반으로 final_estimators 종합하여 예측을 수행

  • 성능을 극으로 끌오올릴 때 활용하기도 함

  • 과대적합을 유발할 수 있다. (특히, 데이터셋이 적은 경우)


[sklearn.ensemble.StackingRegressor] Document

1
from sklearn.ensemble import StackingRegressor
1
2
3
4
5
stack_models = [
    ('elasticnet', poly_elasticnet),
    ('randomforest', rfr_t),
    ('lgbm', lgbm_t)
]
1
2
3
4
stack_reg = StackingRegressor(stack_models, final_estimator=xgb, n_jobs=-1)
stack_reg.fit(x_train, y_train)
stack_pred = stack_reg.predict(x_test)
mse_eval('Stacking Ensemble', y_test, stack_pred)

output_171_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                   Stacking Ensemble  16.906090
9                                             XGBoost  13.841454
10                              RandomForest Ensemble  13.781191
11                             GradientBoost Ensemble  13.451877
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
13                                           LightGBM  12.882170
14  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
15                                 LightGBM w/ Tuning  12.200040
16                                  XGBoost w/ Tuning  11.987602
17                    RandomForest Ensemble w/ Tuning  11.481491

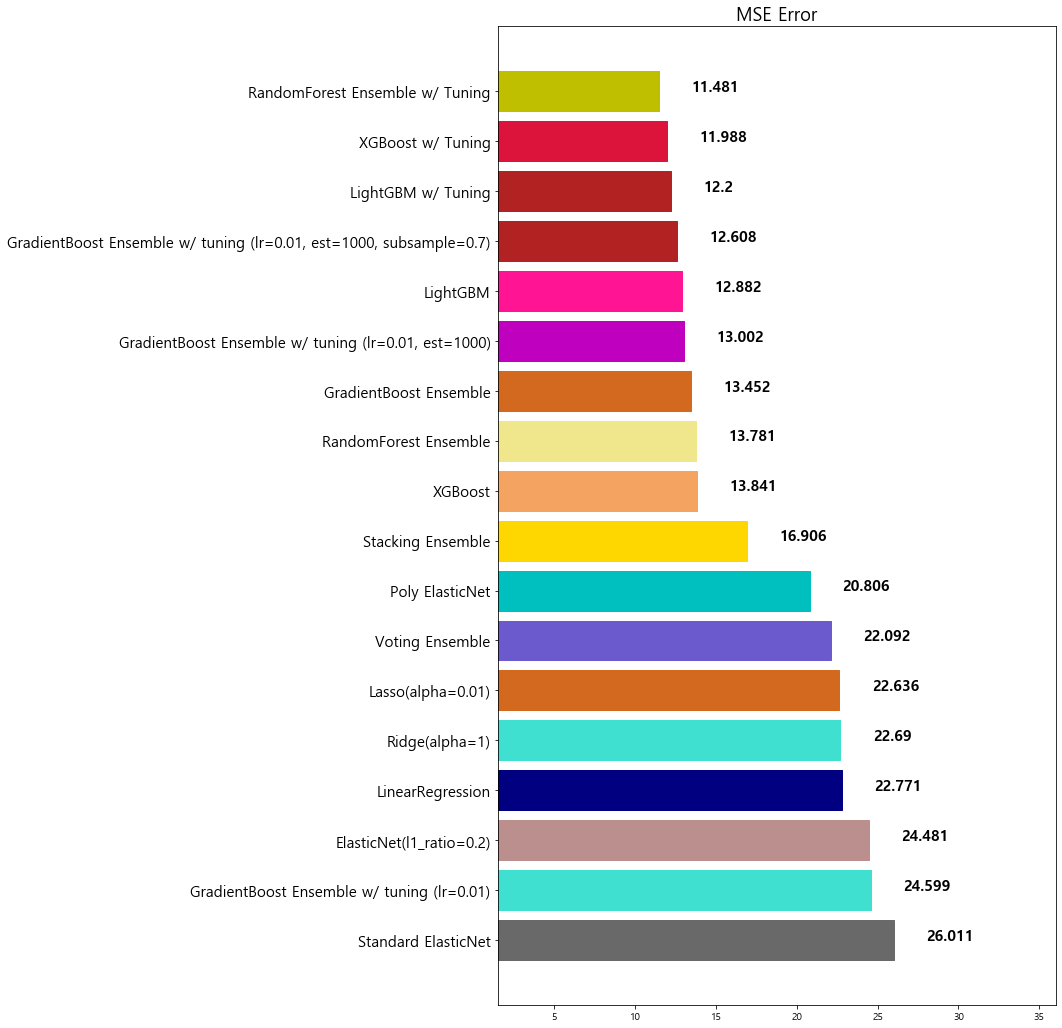
output_171_2


4-5. Weighted Blending

각 모델의 예측값에 대하여 weight를 곱해혀 최종 output 산출

  • 모델에 대한 가중치를 조절하여, 최종 output을 산출함

  • 가중치의 합은 1.0이 되도록 설정


1
2
3
4
5
final_outputs = {
    'randomforest': rfr_t_pred,
    'xgboost': xgb_t_pred,
    'lgbm': lgbm_t_pred
}
1
2
3
4
final_prediction=\
final_outputs['randomforest'] * 0.5\
+final_outputs['xgboost'] * 0.3\
+final_outputs['lgbm'] * 0.2\
1
mse_eval('Weighted Blending', y_test, final_prediction)

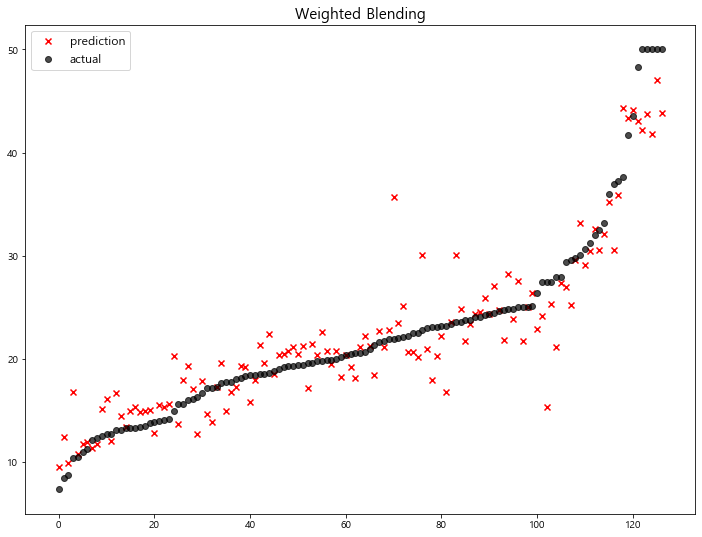
output_178_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                   Stacking Ensemble  16.906090
9                                             XGBoost  13.841454
10                              RandomForest Ensemble  13.781191
11                             GradientBoost Ensemble  13.451877
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
13                                           LightGBM  12.882170
14  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
15                                 LightGBM w/ Tuning  12.200040
16                                  XGBoost w/ Tuning  11.987602
17                    RandomForest Ensemble w/ Tuning  11.481491
18                                  Weighted Blending  10.585610

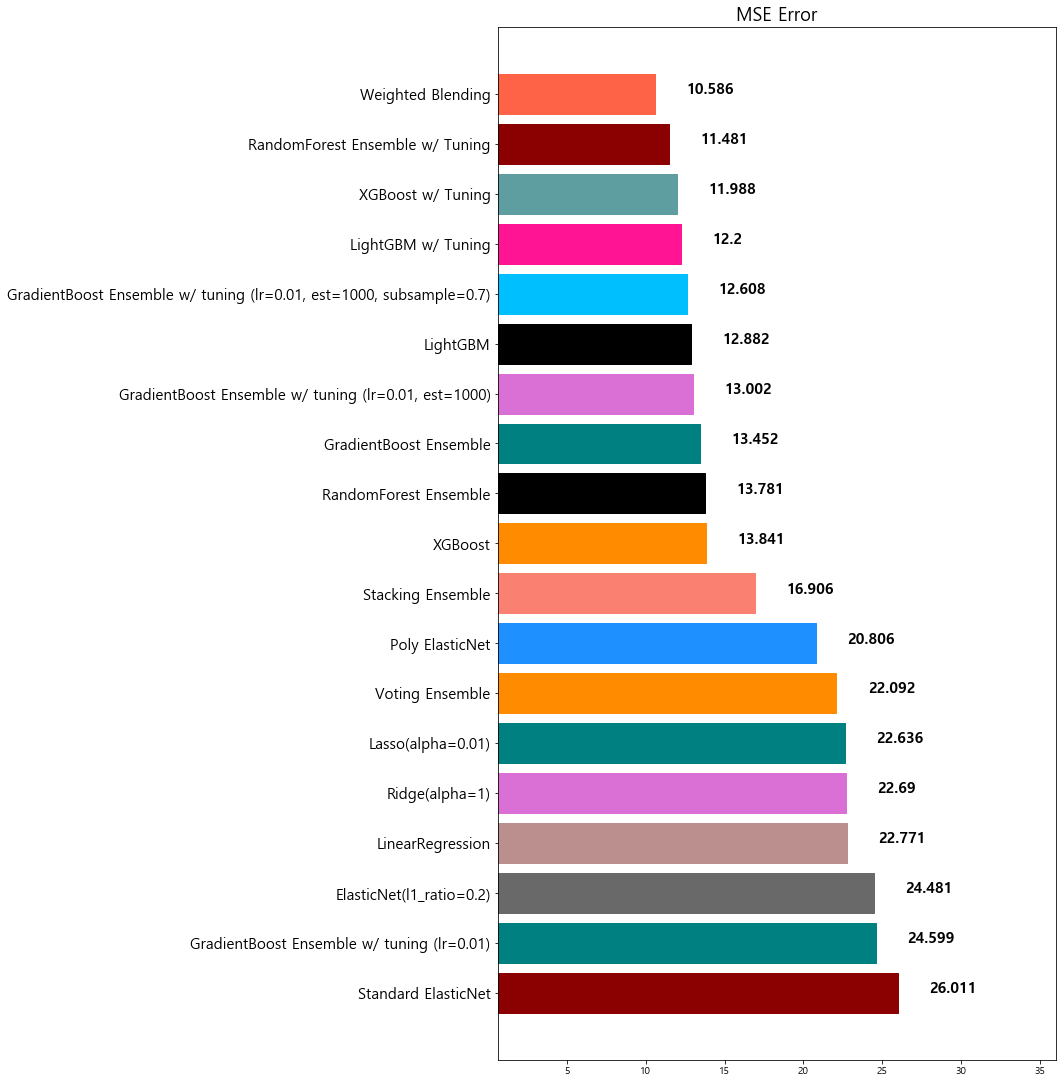
output_178_2


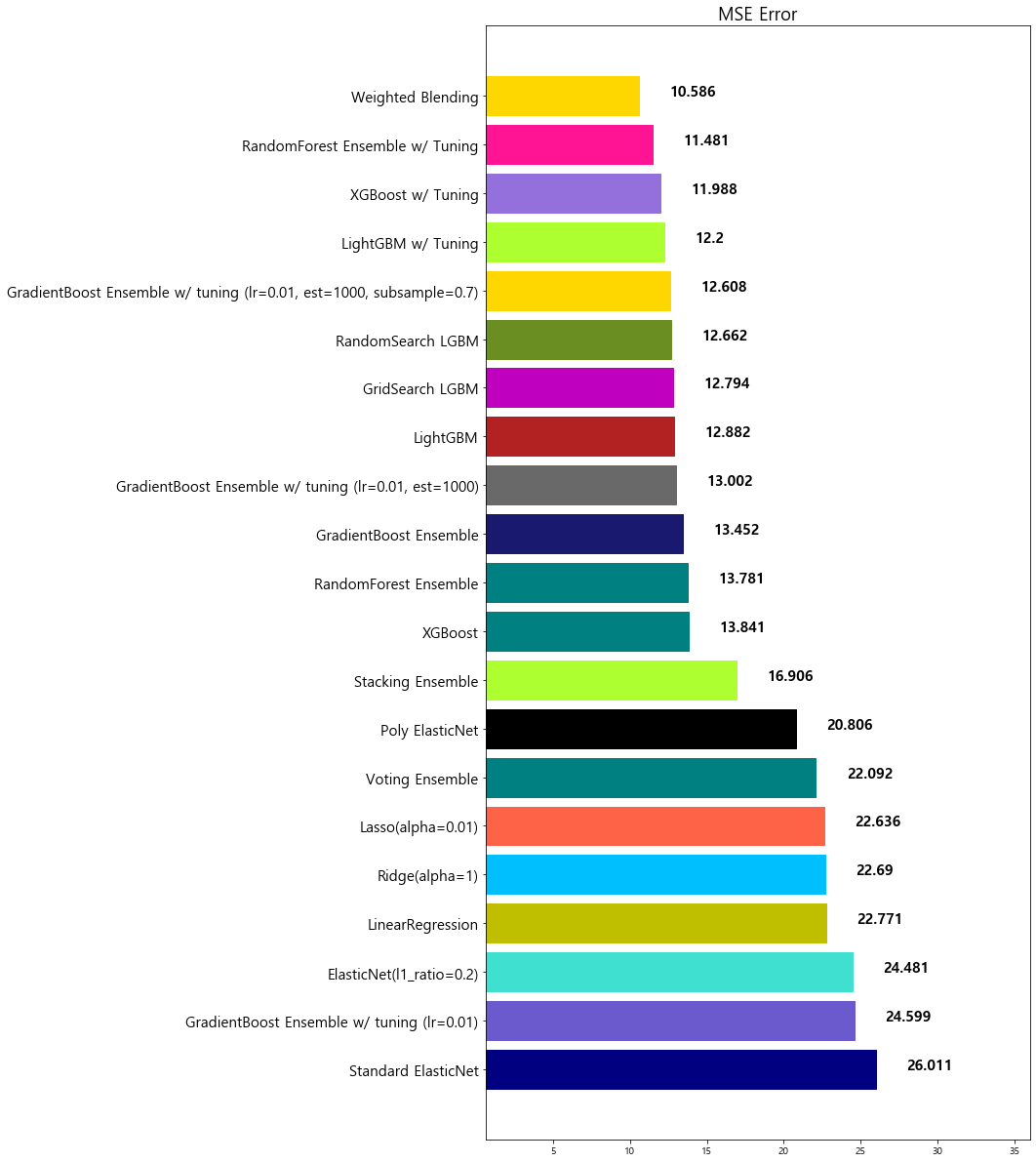
4-6. 앙상블 모델 정리

  1. 앙상블은 대체적으로 단일 모델 대비 성능이 좋다

  2. 앙상블을 앙상블하는 기법인 Stacking과 Weighted Blending도 참고해 볼만 하다

  3. 앙상블 모델은 적절한 Hyper-parameter Tuning이 중요하다

  4. 앙상블 모델은 대체적으로 학습시간이 더 오래 걸린다

  5. 따라서, 모델 튜닝을 하는 데에 시간이 오래 소유된다



5. Cross Validation

5-1. Cross Validation 소개

Cross Validation 알아보기

참고 자료: 딥러닝 모델의 K-겹 교차검증 (K-fold Cross Validation)

전에 진행했던 실습에서도 보였듯이, Hyper-parameter의 값은 모델의 성능을 좌우한다. 그러므로 예측 모델의 성능을 높이기 위해, Hyper-parameter Tuning이 매우 중요하다.

  • 이를 실현하기 위해 저희는 Training data을 다시 Training set과 Validation set으로 나눈다. Trainging set에서 Hyper-parameter값을 바뀌가면서 모델 학습하고, Validation set에서 모델의 성능을 평가하여, 모델 성능을 제일 높일 수 있는 Hyper-parameter값을 선택한다

  • 하지만, 데이터의 일부만 Validation set으로 사용해 모델 성능을 평가하게 되면, 훈련된 모델이 Test set에 대한 성능 평가의 신뢰성이 떨어질 수 있다. 이를 방지하기 위해 **K-fold Cross Validation (K-겹 교차검증)**을 많이 활용한다

    • K겹 교차 검증은 모든 데이터가 최소 한 번은 validation set으로 쓰이도록 한다
      (아래의 그림을 보면, 데이터를 5개로 쪼개 매번 validation set을 바꿔나가는 것을 볼 수 있다)
    • K번 검증을 통해 구한 K 개의 평가지표 값을 평균 내어 모델 성능을 평가한다

CV


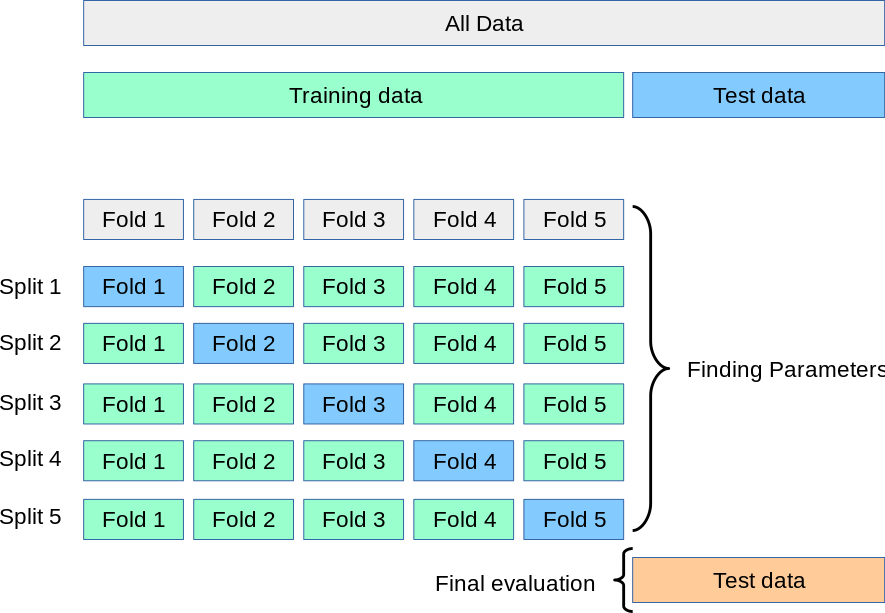
[예시]

  • Estimation 1일 때,
    Training set: [2, 3, 4, 5] / Validation set: [1]

  • Estimation 2일 때,
    Training set: [1, 3, 4, 5] / Validation set: [2]


1
from sklearn.model_selection import KFold
1
2
n_splits = 5
kfold = KFold(n_splits=n_splits, random_state=1, shuffle = True)
1
df.head()
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT MEDV
0 0.00632 18.0 2.31 0.0 0.538 6.575 65.2 4.0900 1.0 296.0 15.3 396.90 4.98 24.0
1 0.02731 0.0 7.07 0.0 0.469 6.421 78.9 4.9671 2.0 242.0 17.8 396.90 9.14 21.6
2 0.02729 0.0 7.07 0.0 0.469 7.185 61.1 4.9671 2.0 242.0 17.8 392.83 4.03 34.7
3 0.03237 0.0 2.18 0.0 0.458 6.998 45.8 6.0622 3.0 222.0 18.7 394.63 2.94 33.4
4 0.06905 0.0 2.18 0.0 0.458 7.147 54.2 6.0622 3.0 222.0 18.7 396.90 5.33 36.2 
1
2
X = np.array(df.drop('MEDV', 1))
Y = np.array(df['MEDV'])
1
lgbm_fold = LGBMRegressor(random_state=1)
1
2
3
4
5
6
7
8
9
10
11
12
i = 1
total_error = 0
for train_index, test_index in kfold.split(X):
    x_train_fold, x_test_fold = X[train_index], X[test_index]
    y_train_fold, y_test_fold = Y[train_index], Y[test_index]
    lgbm_fold_pred = lgbm_fold.fit(x_train_fold, y_train_fold).predict(x_test_fold)
    error = mean_squared_error(y_test_fold, lgbm_fold_pred)
    print('Fold = {}, prediction score = {:.2f}'.format(i, error))
    total_error += error
    i+=1
print('---'*10)
print('Average Error: %s' % (total_error / n_splits))
Fold = 1, prediction score = 9.76
Fold = 2, prediction score = 20.58
Fold = 3, prediction score = 6.95
Fold = 4, prediction score = 12.18
Fold = 5, prediction score = 10.87
------------------------------
Average Error: 12.06743160435072

5-2. Hyper-parameter 튜닝

Hyper-parameter 튜닝 시 경우의 수가 너무 많으므로 우리는 자동화할 틸요가 있다

sklearn 패키지에서 자주 사용되는 hyper-parameter 튜닝을 돕는 클래스는 다음 2가지가 있다:

  1. RandomizedSerchCV
  2. GridSerchCV

적용하는 방법

  1. 사용할 Search 방법을 선택한다

  2. hyper-parameter 도메인(값의 범위)을 설정한다 (max_depth, n_estimators… 등등)

  3. 학습을 시킨 후, 기다린다

  4. 도출된 결과 값을 모델에 적용하고 성능을 비교한다


(1) RandomizedSearchCV

  • 모든 매개 변수 값이 시도되는 것이 아니라 지정된 분포에서 고정 된 수의 매개 변수 설정이 샘플링된다.

  • 시도 된 매개 변수 설정의 수는 n_iter에 의해 제공됨.


주요 Hyper-parameter (LGBM)

  • random_state: random seed 고정 값
  • n_jobs: CPU 사용 갯수
  • learning_rate: 학습율. 너무 큰 학습율은 성능을 떨어뜨리고, 너무 작은 학습율은 학습이 느리다. 적절한 값을 찾아야함. n_estimators와 같이 튜닝. default=0.1
  • n_estimators: 부스팅 스테이지 수. (랜덤포레스트 트리의 갯수 설정과 비슷한 개념). default=100
  • max_depth: 트리의 깊이. 과대적합 방지용. default=3.
  • colsample_bytree: 샘플 사용 비율 (max_features와 비슷한 개념). 과대적합 방지용. default=1.0
1
2
3
4
5
6
7
params = {
    'learning_rate': [0.005, 0.01, 0.03, 0.05],
    'n_estimators': [500, 1000, 2000, 3000],
    'max_depth': [3, 5, 7],
    'colsample_bytree': [0.8, 0.9, 1.0],
    'subsample': [0.7, 0.8, 0.9, 1.0],
}
1
from sklearn.model_selection import RandomizedSearchCV
조절하여, 총 몇 회의 시도를 진행할 것인자 정의한다 
1
2
3
4
5
(회수가 늘어나면, 더 좋은 parameter를 찾을 확률은 올라가지만, 그만큼 시간이 오래걸린다.)


```python
rcv_lgbm = RandomizedSearchCV(LGBMRegressor(), params, random_state=1, cv=5, n_iter=100, scoring='neg_mean_squared_error')
1
rcv_lgbm.fit(x_train, y_train)
RandomizedSearchCV(cv=5, error_score=nan,
                   estimator=LGBMRegressor(boosting_type='gbdt',
                                           class_weight=None,
                                           colsample_bytree=1.0,
                                           importance_type='split',
                                           learning_rate=0.1, max_depth=-1,
                                           min_child_samples=20,
                                           min_child_weight=0.001,
                                           min_split_gain=0.0, n_estimators=100,
                                           n_jobs=-1, num_leaves=31,
                                           objective=None, random_state=None,
                                           reg_alpha=0.0, reg_lambda=0.0,
                                           silen...
                                           subsample_freq=0),
                   iid='deprecated', n_iter=100, n_jobs=None,
                   param_distributions={'colsample_bytree': [0.8, 0.9, 1.0],
                                        'learning_rate': [0.005, 0.01, 0.03,
                                                          0.05],
                                        'max_depth': [3, 5, 7],
                                        'n_estimators': [500, 1000, 2000, 3000],
                                        'subsample': [0.7, 0.8, 0.9, 1.0]},
                   pre_dispatch='2*n_jobs', random_state=1, refit=True,
                   return_train_score=False, scoring='neg_mean_squared_error',
                   verbose=0)

1
rcv_lgbm.best_score_
-11.132039701508374

1
rcv_lgbm.best_params_
{'subsample': 0.8,
 'n_estimators': 1000,
 'max_depth': 3,
 'learning_rate': 0.05,
 'colsample_bytree': 0.9}

1
2
3
lgbm_best = LGBMRegressor(learning_rate=0.05, n_estimators=1000, subsample=0.8, max_depth=3, colsample_bytree=0.9)
lgbm_best_pred = lgbm_best.fit(x_train, y_train).predict(x_test)
mse_eval('RandomSearch LGBM', y_test, lgbm_best_pred)

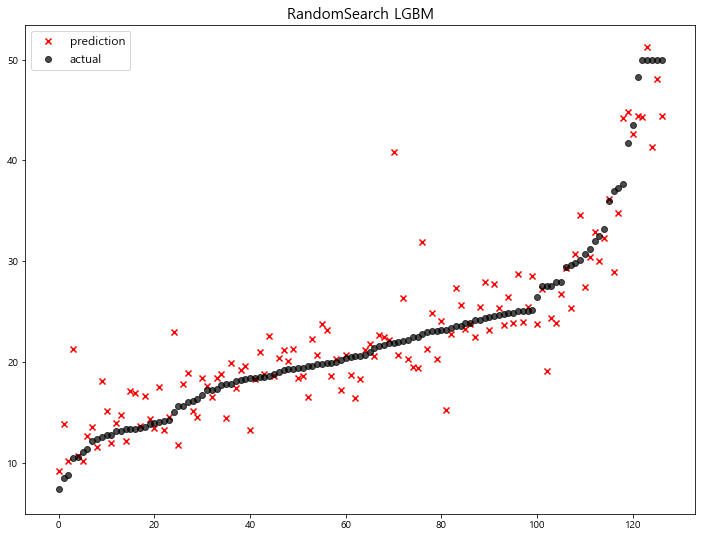
output_216_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                   Stacking Ensemble  16.906090
9                                             XGBoost  13.841454
10                              RandomForest Ensemble  13.781191
11                             GradientBoost Ensemble  13.451877
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
13                                           LightGBM  12.882170
14                                  RandomSearch LGBM  12.661917
15  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
16                                 LightGBM w/ Tuning  12.200040
17                                  XGBoost w/ Tuning  11.987602
18                    RandomForest Ensemble w/ Tuning  11.481491
19                                  Weighted Blending  10.585610

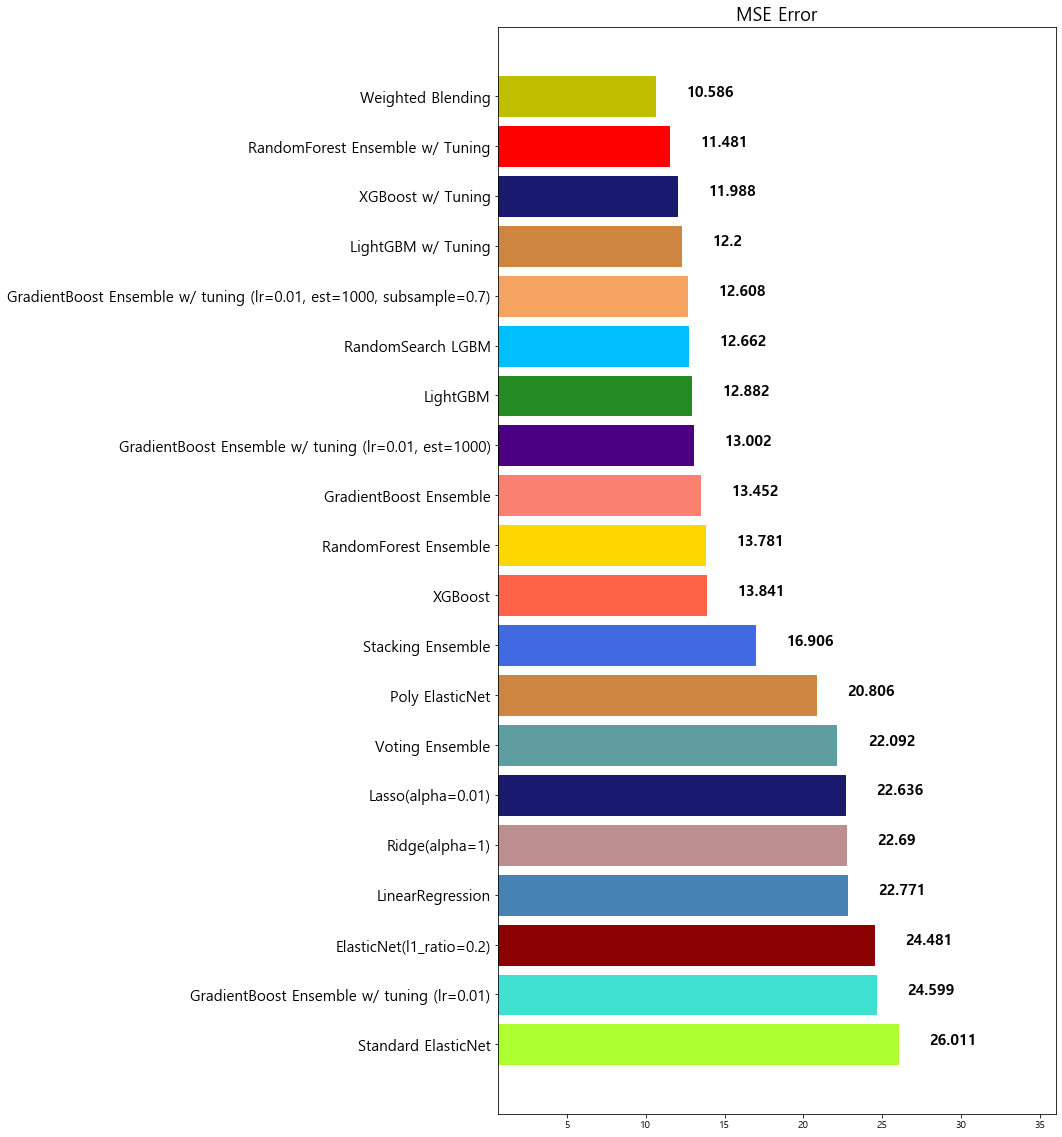
output_216_2


(2) GridSerchCV

  • 모든 매개 변수 값에 대하여 완전 탐색을 시도한다
  • 따라서, 최적화할 parameter가 많다면, 시간이 매우 오래걸린다
1
2
3
4
5
6
7
params = {
    'learning_rate': [0.04, 0.05, 0.06],
    'n_estimators': [800, 1000, 1200],
    'max_depth': [3, 4, 5],
    'colsample_bytree': [0.8, 0.85, 0.9],
    'subsample': [0.8, 0.85, 0.9],
}
1
from sklearn.model_selection import GridSearchCV
1
grid_search = GridSearchCV(LGBMRegressor(), params, cv=5, n_jobs=-1, scoring='neg_mean_squared_error')
1
grid_search.fit(x_train, y_train)
GridSearchCV(cv=5, error_score=nan,
             estimator=LGBMRegressor(boosting_type='gbdt', class_weight=None,
                                     colsample_bytree=1.0,
                                     importance_type='split', learning_rate=0.1,
                                     max_depth=-1, min_child_samples=20,
                                     min_child_weight=0.001, min_split_gain=0.0,
                                     n_estimators=100, n_jobs=-1, num_leaves=31,
                                     objective=None, random_state=None,
                                     reg_alpha=0.0, reg_lambda=0.0, silent=True,
                                     subsample=1.0, subsample_for_bin=200000,
                                     subsample_freq=0),
             iid='deprecated', n_jobs=-1,
             param_grid={'colsample_bytree': [0.8, 0.85, 0.9],
                         'learning_rate': [0.04, 0.05, 0.06],
                         'max_depth': [3, 4, 5],
                         'n_estimators': [800, 1000, 1200],
                         'subsample': [0.8, 0.85, 0.9]},
             pre_dispatch='2*n_jobs', refit=True, return_train_score=False,
             scoring='neg_mean_squared_error', verbose=0)

1
grid_search.best_score_
-11.10039780445118

1
grid_search.best_params_
{'colsample_bytree': 0.9,
 'learning_rate': 0.05,
 'max_depth': 3,
 'n_estimators': 800,
 'subsample': 0.8}

1
2
3
lgbm_best = LGBMRegressor(learning_rate=0.05, n_estimators=800, subsample=0.8, max_depth=3, colsample_bytree=0.9)
lgbm_best_pred = lgbm_best.fit(x_train, y_train).predict(x_test)
mse_eval('GridSearch LGBM', y_test, lgbm_best_pred)

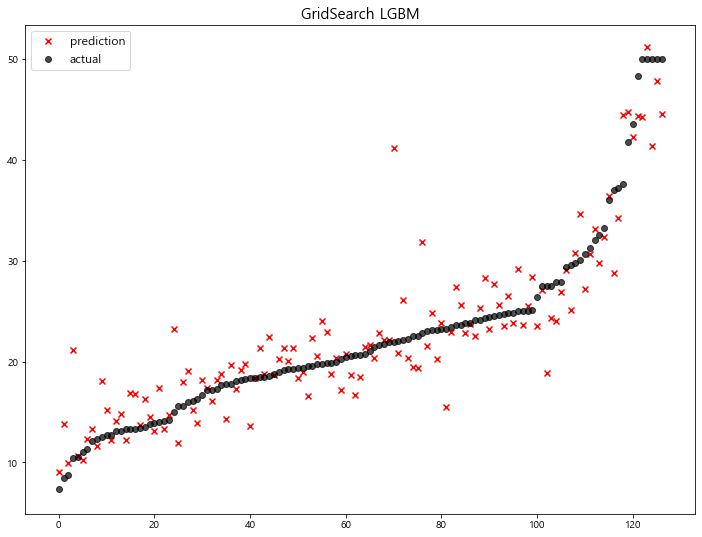
output_226_0

                                                model        mse
0                                 Standard ElasticNet  26.010756
1          GradientBoost Ensemble w/ tuning (lr=0.01)  24.599441
2                            ElasticNet(l1_ratio=0.2)  24.481069
3                                    LinearRegression  22.770784
4                                      Ridge(alpha=1)  22.690411
5                                   Lasso(alpha=0.01)  22.635614
6                                     Voting Ensemble  22.092158
7                                     Poly ElasticNet  20.805986
8                                   Stacking Ensemble  16.906090
9                                             XGBoost  13.841454
10                              RandomForest Ensemble  13.781191
11                             GradientBoost Ensemble  13.451877
12  GradientBoost Ensemble w/ tuning (lr=0.01, est...  13.002472
13                                           LightGBM  12.882170
14                                    GridSearch LGBM  12.794172
15                                  RandomSearch LGBM  12.661917
16  GradientBoost Ensemble w/ tuning (lr=0.01, est...  12.607717
17                                 LightGBM w/ Tuning  12.200040
18                                  XGBoost w/ Tuning  11.987602
19                    RandomForest Ensemble w/ Tuning  11.481491
20                                  Weighted Blending  10.585610

output_226_2