【EDA & Regression 실습】 – 부동산 데이터


0. 개요

미국 매사추세츠주의 주택 가격 데이터(Boston Housing 1970)를 활용해 지역의 평균 주택 가격을 예측하는 선형 회귀 모델을 만들었고, 이를 기초하여 주택 가격의 영향 요소 파악 및 주택 가격 예측을 진행하였습니다.

전체 분석 절차는 다음과 같습니다:

  1. 데이터 파악 (EDA: 탐색적 데이터 분석)

    • 데이터셋 기본 정보 파악
    • 변수 특징 탐색
    • 변수간 관계 탐색

  2. 데이터 전처리

  3. 모델링

  4. 주택 가격 영향 요소 파악

  5. 주택 가격 예측 및 모델 예측 성능 평가


1. Library & Data Import

>> 사용할 Library

1
2
3
4
5
6
7
8
9
%matplotlib inline

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

import warnings
warnings.filterwarnings('ignore')

>> 사용할 데이터셋 – Boston Housing Dataset

분석에 사용될 데이터셋은 Boston Housing 1970데이터의 일부 변수를 추출한 데이터입니다.
여기에 미국 매사추세츠주 92개 도시(TOWN)의 506개 지역의 주택 가격 및 기타 지역 특성 데이터가 포함되어 있습니다. (Dataset Introduction)

데이터셋을 불러와서 첫 다섯 줄을 출력하여 데이터의 구성을 한 번 살펴볼게요.

1
df = pd.read_csv("https://raw.githubusercontent.com/yoonkt200/FastCampusDataset/master/BostonHousing2.csv")
1
df.head()
TOWN LON LAT CMEDV CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 Nahant -70.955 42.2550 24.0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
1 Swampscott -70.950 42.2875 21.6 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
2 Swampscott -70.936 42.2830 34.7 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
3 Marblehead -70.928 42.2930 33.4 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
4 Marblehead -70.922 42.2980 36.2 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33

>> Feature Description

각 변수의 의미는 다음과 같습니다:

  • TOWN: 소속 도시 이름

  • LON, LAT: 해당 지역의 경도(Longitudes) 위도(Latitudes) 정보

  • CMEDV: 해당 지역의 주택 가격 (중앙값) (corrected median values of housing in USD 1000)

  • CRIM: 지역 범죄율 (per capita crime)

  • ZN: 소속 도시에 25,000 제곱 피트(sq.ft) 이상의 주택지 비율

  • INDUS: 소속 도시에 상업적 비즈니스에 활용되지 않는 농지 면적

  • CHAS: 해당 지역이 Charles 강과 접하고 있는지 여부 (dummy variable)

  • NOX: 소속 도시의 산화질소 농도

  • RM: 해당 지역의 자택당 평균 방 갯수

  • AGE: 해당 지역에 1940년 이전에 건설된 주택의 비율

  • DIS: 5개의 보스턴 고용 센터와의 거리에 따른 가중치 부여

  • RAD: 소속 도시가 Radial 고속도로와의 접근성 지수

  • TAX: 소속 도시의 10000달러당 재산세

  • PTRATIO: 소속 도시의 학생-교사 비율

  • B: 해당 지역의 흑인 지수 (1000(Bk - 0.63)^2), Bk는 흑인의 비율

  • LSTAT: 해당 지역의 빈곤층 비율



2. 데이터 파악 (EDA: 탐색적 데이터 분석)

이제 데이터셋의 기본 정보 및 각 변수의 특성을 파악해 보겠습니다.

1
2
# 그래프 배경 설정
sns.set_style('darkgrid')

2-1. 데이터셋 기본 정보 파악

먼저 데이터셋의 기본 정보부터 알아볼게요.

1
2
# shape (dimension)
df.shape
(506, 17)


1
2
# 결측치
df.isnull().sum()
TOWN       0
LON        0
LAT        0
CMEDV      0
CRIM       0
ZN         0
INDUS      0
CHAS       0
NOX        0
RM         0
AGE        0
DIS        0
RAD        0
TAX        0
PTRATIO    0
B          0
LSTAT      0
dtype: int64

데이터셋은 총 506개의 관측치(observations)과 17개의 변수(variables)로 구성되어 있고 결측치는 존재하지 않습니다.

각 변수의 타입 및 기초 통계량 (범주형 변수는 범주 구성) 을 확인 해보면 다음과 같습니다.

1
2
# data type
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 17 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   TOWN     506 non-null    object 
 1   LON      506 non-null    float64
 2   LAT      506 non-null    float64
 3   CMEDV    506 non-null    float64
 4   CRIM     506 non-null    float64
 5   ZN       506 non-null    float64
 6   INDUS    506 non-null    float64
 7   CHAS     506 non-null    int64  
 8   NOX      506 non-null    float64
 9   RM       506 non-null    float64
 10  AGE      506 non-null    float64
 11  DIS      506 non-null    float64
 12  RAD      506 non-null    int64  
 13  TAX      506 non-null    int64  
 14  PTRATIO  506 non-null    float64
 15  B        506 non-null    float64
 16  LSTAT    506 non-null    float64
dtypes: float64(13), int64(3), object(1)
memory usage: 67.3+ KB

이중 TOWN(소속 도시 이름)만 문자형 변수이고, 이를 제외한 모든 변수가 숫자형 변수입니다.


1
2
# numerical variable
df.describe()
LON LAT CMEDV CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
count 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000 506.000000
mean -71.056389 42.216440 22.528854 3.613524 11.363636 11.136779 0.069170 0.554695 6.284634 68.574901 3.795043 9.549407 408.237154 18.455534 356.674032 12.653063
std 0.075405 0.061777 9.182176 8.601545 23.322453 6.860353 0.253994 0.115878 0.702617 28.148861 2.105710 8.707259 168.537116 2.164946 91.294864 7.141062
min -71.289500 42.030000 5.000000 0.006320 0.000000 0.460000 0.000000 0.385000 3.561000 2.900000 1.129600 1.000000 187.000000 12.600000 0.320000 1.730000
25% -71.093225 42.180775 17.025000 0.082045 0.000000 5.190000 0.000000 0.449000 5.885500 45.025000 2.100175 4.000000 279.000000 17.400000 375.377500 6.950000
50% -71.052900 42.218100 21.200000 0.256510 0.000000 9.690000 0.000000 0.538000 6.208500 77.500000 3.207450 5.000000 330.000000 19.050000 391.440000 11.360000
75% -71.019625 42.252250 25.000000 3.677082 12.500000 18.100000 0.000000 0.624000 6.623500 94.075000 5.188425 24.000000 666.000000 20.200000 396.225000 16.955000
max -70.810000 42.381000 50.000000 88.976200 100.000000 27.740000 1.000000 0.871000 8.780000 100.000000 12.126500 24.000000 711.000000 22.000000 396.900000 37.970000 

1
2
3
4
# categorical variable
num_town = df['TOWN'].unique()
print(len(num_town))
num_town
92



array(['Nahant', 'Swampscott', 'Marblehead', 'Salem', 'Lynn', 'Sargus',
       'Lynnfield', 'Peabody', 'Danvers', 'Middleton', 'Topsfield',
       'Hamilton', 'Wenham', 'Beverly', 'Manchester', 'North Reading',
       'Wilmington', 'Burlington', 'Woburn', 'Reading', 'Wakefield',
       'Melrose', 'Stoneham', 'Winchester', 'Medford', 'Malden',
       'Everett', 'Somerville', 'Cambridge', 'Arlington', 'Belmont',
       'Lexington', 'Bedford', 'Lincoln', 'Concord', 'Sudbury', 'Wayland',
       'Weston', 'Waltham', 'Watertown', 'Newton', 'Natick', 'Framingham',
       'Ashland', 'Sherborn', 'Brookline', 'Dedham', 'Needham',
       'Wellesley', 'Dover', 'Medfield', 'Millis', 'Norfolk', 'Walpole',
       'Westwood', 'Norwood', 'Sharon', 'Canton', 'Milton', 'Quincy',
       'Braintree', 'Randolph', 'Holbrook', 'Weymouth', 'Cohasset',
       'Hull', 'Hingham', 'Rockland', 'Hanover', 'Norwell', 'Scituate',
       'Marshfield', 'Duxbury', 'Pembroke', 'Boston Allston-Brighton',
       'Boston Back Bay', 'Boston Beacon Hill', 'Boston North End',
       'Boston Charlestown', 'Boston East Boston', 'Boston South Boston',
       'Boston Downtown', 'Boston Roxbury', 'Boston Savin Hill',
       'Boston Dorchester', 'Boston Mattapan', 'Boston Forest Hills',
       'Boston West Roxbury', 'Boston Hyde Park', 'Chelsea', 'Revere',
       'Winthrop'], dtype=object)

2-2. 종속 변수(목표 변수) 탐색

>> Target Variable: ‘CMEDV’(주택 가격) 탐색

이제 각 변수의 특성을 시각화 도구를 통해 파악해보겠습니다.
먼저 우리가 예측하고자 하는 대상, 즉 회귀 모델의 종속 변수인 “주택 가격”(‘CMECV’) 부터 살펴볼게요.

1
2
# 기초 통계량
df['CMEDV'].describe()
count    506.000000
mean      22.528854
std        9.182176
min        5.000000
25%       17.025000
50%       21.200000
75%       25.000000
max       50.000000
Name: CMEDV, dtype: float64


1
2
# 분포
df['CMEDV'].hist(bins=50)
<matplotlib.axes._subplots.AxesSubplot at 0x1ca69ebcf48>

png

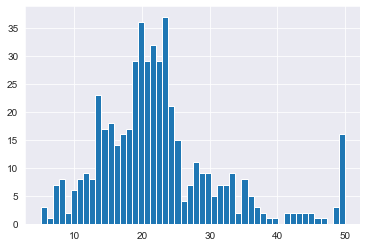
boxplot:

  1. Pandas Function (pandas.DataFrame.boxplot)
  2. Matplotlib Function (matplotlib.pyplot.boxplot)
1
2
3
# boxplot - Pandas
df.boxplot(column=['CMEDV'])
plt.show()

png


1
2
3
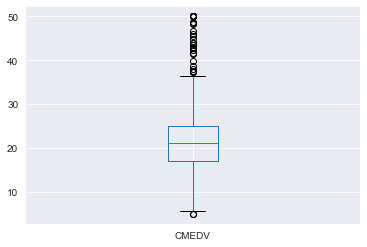
# boxplot - matplotlib
plt.boxplot(df['CMEDV'])
plt.show()

png

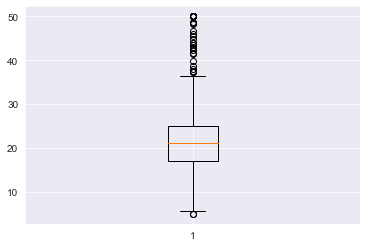
분포를 살펴보면, 주택 가격이 대부분 $17,000 ~ $25,000 사이에 분포되어 있으며, 소수의 $40,000 이상인 고가 주택도 존재합니다.


2-3. 설명 변수 탐색

>> 설명 변수의 분포 탐색

1
2
3
4
5
6
7
8
# numerical features (except "LON" & "LAT")
numerical_columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']

fig = plt.figure(figsize = (16, 20))
ax = fig.gca()  # Axes 생성

df[numerical_columns].hist(ax=ax)
plt.show()

png


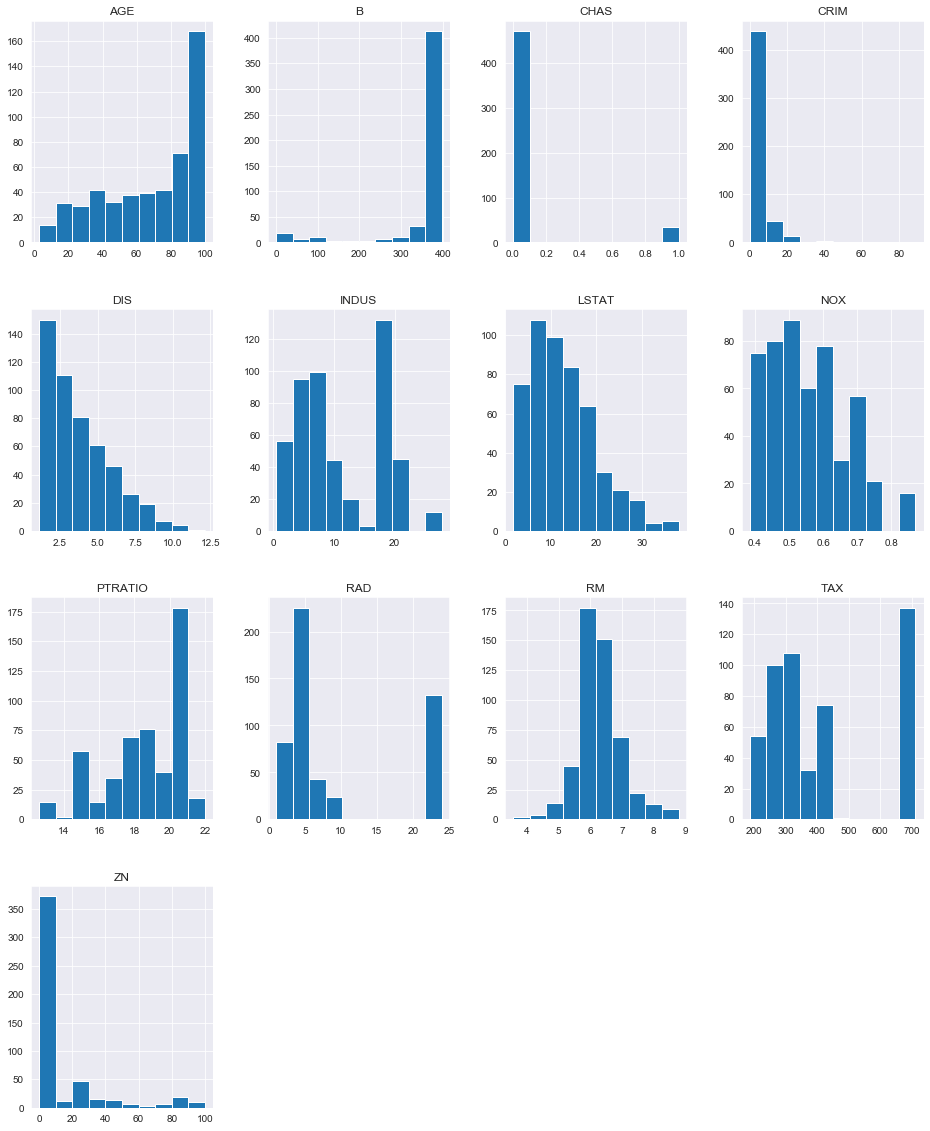
2-4. 설명변수와 종속변수 간의 관계 탐색

>> 변수간의 상관계수 파악

먼저 변수간의 상관계수를 추출해보겠습니다.

1
2
3
4
5
# Person 상관계수
cols = ['CMEDV', 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']

corr = df[cols].corr(method = 'pearson')
corr
CMEDV CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
CMEDV 1.000000 -0.389582 0.360386 -0.484754 0.175663 -0.429300 0.696304 -0.377999 0.249315 -0.384766 -0.471979 -0.505655 0.334861 -0.740836
CRIM -0.389582 1.000000 -0.200469 0.406583 -0.055892 0.420972 -0.219247 0.352734 -0.379670 0.625505 0.582764 0.289946 -0.385064 0.455621
ZN 0.360386 -0.200469 1.000000 -0.533828 -0.042697 -0.516604 0.311991 -0.569537 0.664408 -0.311948 -0.314563 -0.391679 0.175520 -0.412995
INDUS -0.484754 0.406583 -0.533828 1.000000 0.062938 0.763651 -0.391676 0.644779 -0.708027 0.595129 0.720760 0.383248 -0.356977 0.603800
CHAS 0.175663 -0.055892 -0.042697 0.062938 1.000000 0.091203 0.091251 0.086518 -0.099176 -0.007368 -0.035587 -0.121515 0.048788 -0.053929
NOX -0.429300 0.420972 -0.516604 0.763651 0.091203 1.000000 -0.302188 0.731470 -0.769230 0.611441 0.668023 0.188933 -0.380051 0.590879
RM 0.696304 -0.219247 0.311991 -0.391676 0.091251 -0.302188 1.000000 -0.240265 0.205246 -0.209847 -0.292048 -0.355501 0.128069 -0.613808
AGE -0.377999 0.352734 -0.569537 0.644779 0.086518 0.731470 -0.240265 1.000000 -0.747881 0.456022 0.506456 0.261515 -0.273534 0.602339
DIS 0.249315 -0.379670 0.664408 -0.708027 -0.099176 -0.769230 0.205246 -0.747881 1.000000 -0.494588 -0.534432 -0.232471 0.291512 -0.496996
RAD -0.384766 0.625505 -0.311948 0.595129 -0.007368 0.611441 -0.209847 0.456022 -0.494588 1.000000 0.910228 0.464741 -0.444413 0.488676
TAX -0.471979 0.582764 -0.314563 0.720760 -0.035587 0.668023 -0.292048 0.506456 -0.534432 0.910228 1.000000 0.460853 -0.441808 0.543993
PTRATIO -0.505655 0.289946 -0.391679 0.383248 -0.121515 0.188933 -0.355501 0.261515 -0.232471 0.464741 0.460853 1.000000 -0.177383 0.374044
B 0.334861 -0.385064 0.175520 -0.356977 0.048788 -0.380051 0.128069 -0.273534 0.291512 -0.444413 -0.441808 -0.177383 1.000000 -0.366087
LSTAT -0.740836 0.455621 -0.412995 0.603800 -0.053929 0.590879 -0.613808 0.602339 -0.496996 0.488676 0.543993 0.374044 -0.366087 1.000000

상관계수를 좀 더 직관적인 Heatmap으로 표현해볼게요.

1
2
3
4
5
6
7
8
9
# heatmap (seaborn)
fig = plt.figure(figsize = (16, 12))
ax = fig.gca()

sns.set(font_scale = 1.5)  # heatmap 안의 font-size 설정
heatmap = sns.heatmap(corr.values, annot = True, fmt='.2f', annot_kws={'size':15},
                      yticklabels = cols, xticklabels = cols, ax=ax, cmap = "RdYlBu")
plt.tight_layout()
plt.show()

png

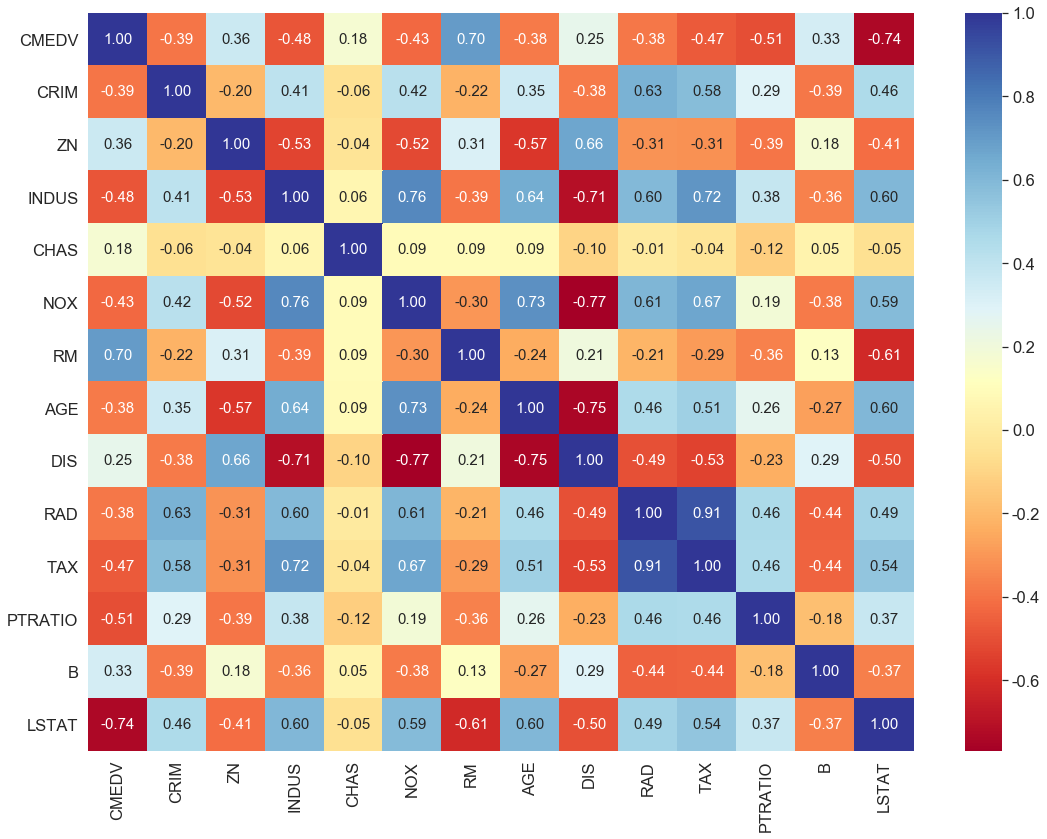
우리의 관심사인 target variable **“CMEDV - 주택 가격”**과 다른 변수간의 상관관계를 살펴보면, **“CMEDV - 주택 가격”**은 “RM - 자택당 평균 방 갯수”(0.7) 및 **“LSTAT - 빈곤층의 비율”(-0.74)**과 강한 상관관계를 보이고 있다는 것을 알 수 있습니다.

이 두 변수와의 관계를 좀 더 자세히 살펴볼게요.


>> 종속 변수와 설명 변수간의 관계 탐색

  • 주택 가격 ( “CMEDV” ) ~ 방 갯수 ( “RM” )
1
2
3
4
# scatter plot
sns.scatterplot(data=df, x='RM', y='CMEDV', markers='o', color='blue', alpha=0.6)
plt.title('Scatter Plot')
plt.show()

png

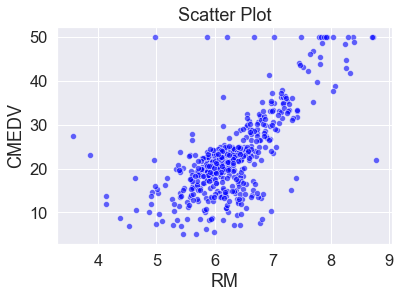
주택 가격이 방 갯수와 양의 상관관계(positive correlation)를 갖고 있습니다. 즉, 방 갯수가 많은 주택들이 상대적으로 더 높은 가격을 갖고 있습니다.


  • 주택 가격(“CMEDV”) ~ 빈곤층의 비율(“LSTAT”)
1
2
3
4
# scatter plot
sns.scatterplot(data=df, x='LSTAT', y='CMEDV', markers='o', color='blue', alpha=0.6)
plt.title('Scatter Plot')
plt.show()

png

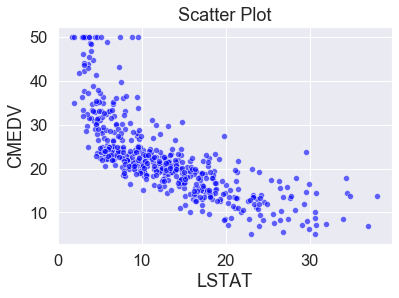
주택 가격이 빈곤층의 비율과 음의 상관관계(negative correlation)를 갖고 있습니다. 즉, 빈곤층의 비율이 높은 지역의 주택 가격이 상대적으로 낮은 경향이 있습니다.


>> 도시별 차이 탐색

데이터를 살펴보면 여러 지역이 같은 도시에 속한 경우가 있습니다. 변수 중에서도 도시 단위로 측정되는 변수가 많고요. 따라서 우리는 자연스럽게 도시 간의 차이를 궁금하게 됩니다.

먼저 각 도시의 데이터 갯수부터 살펴볼게요.

1
2
# 도시별 데이터 갯수
df['TOWN'].value_counts()
Cambridge            30
Boston Savin Hill    23
Lynn                 22
Boston Roxbury       19
Newton               18
                     ..
Hanover               1
Hull                  1
Sherborn              1
Hamilton              1
Dover                 1
Name: TOWN, Length: 92, dtype: int64


1
2
# 도시별 데이터 갯수 (bar plot)
df['TOWN'].value_counts().hist(bins=50)
<matplotlib.axes._subplots.AxesSubplot at 0x1ca6c233a48>

png


이제 각 도시의 주택 가격 분포를 box plot을 통해 표현 해보겠습니다.

1
2
3
# 도시별 주택 가격 특징 (boxplot 이용)
fig = plt.figure(figsize = (12, 20))
sns.boxplot(x='CMEDV', y='TOWN', data=df)
<matplotlib.axes._subplots.AxesSubplot at 0x23cf3ff9ec8>

png

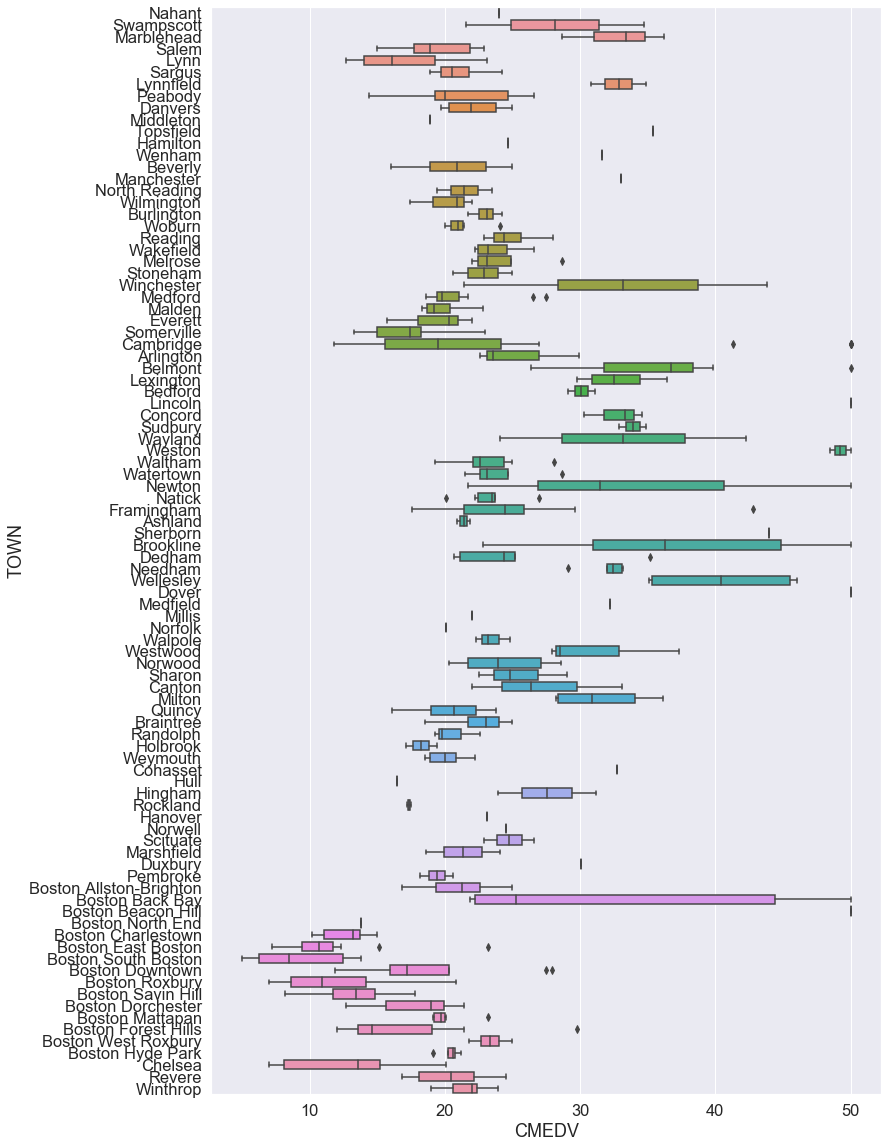
그림을 보면, Boston 지역(Boston으로 시작하는 도시)의 주택 가격이 전반적으로 다른 지역보다 낮다는 것을 알 수 있습니다.

도시별 범죄율을 한 번 확인 해보면,

1
2
3
# 도시별 범죄율 특징
fig = plt.figure(figsize = (12, 20))
sns.boxplot(x='CRIM', y='TOWN', data=df)
<matplotlib.axes._subplots.AxesSubplot at 0x23cf407fec8>

png

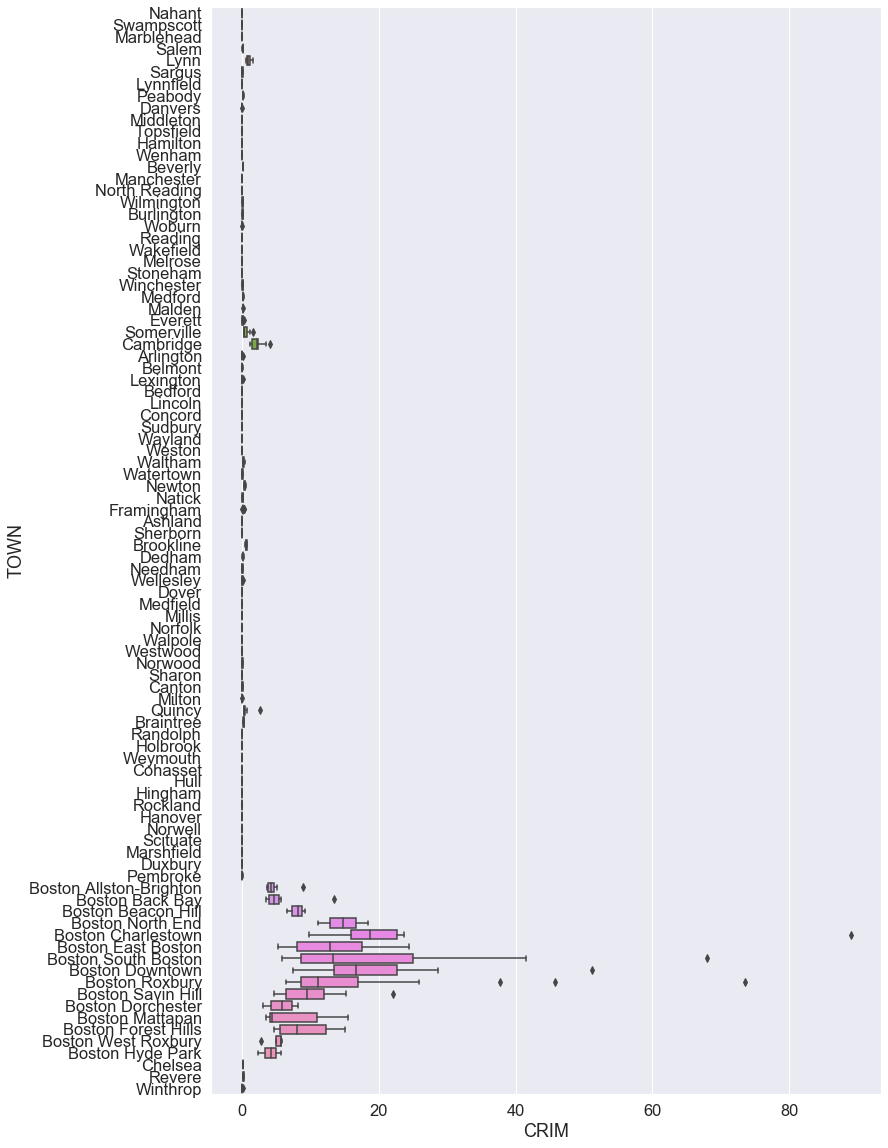
Boston 지역의 범죄율이 유독 높다는 것을 확인할 수 있고, 따라서 범죄율이 높은 지역의 주택 가격이 상대적으로 낮다는 것을 추측해볼 수 있겠습니다.



3. 주택 가격 예측 모델링: 회귀 분석

이제 변수들을 활용하여 매사추세츠주 각 지역의 주택 가격을 예측하는 회귀 모델을 만들어 보겠습니다.

3-1. 데이터 전처리

>> Feature 표준화

먼저 Feature 들의 scale 차이를 없애기 위해 수치형 Feature에 대해서 표준화를 진행해야 합니다.

1
df.head()
TOWN LON LAT CMEDV CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 Nahant -70.955 42.2550 24.0 0.00632 18.0 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98
1 Swampscott -70.950 42.2875 21.6 0.02731 0.0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14
2 Swampscott -70.936 42.2830 34.7 0.02729 0.0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03
3 Marblehead -70.928 42.2930 33.4 0.03237 0.0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94
4 Marblehead -70.922 42.2980 36.2 0.06905 0.0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 

1
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 506 entries, 0 to 505
Data columns (total 17 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   TOWN     506 non-null    object 
 1   LON      506 non-null    float64
 2   LAT      506 non-null    float64
 3   CMEDV    506 non-null    float64
 4   CRIM     506 non-null    float64
 5   ZN       506 non-null    float64
 6   INDUS    506 non-null    float64
 7   CHAS     506 non-null    int64  
 8   NOX      506 non-null    float64
 9   RM       506 non-null    float64
 10  AGE      506 non-null    float64
 11  DIS      506 non-null    float64
 12  RAD      506 non-null    int64  
 13  TAX      506 non-null    int64  
 14  PTRATIO  506 non-null    float64
 15  B        506 non-null    float64
 16  LSTAT    506 non-null    float64
dtypes: float64(13), int64(3), object(1)
memory usage: 67.3+ KB


문자형 변수인 "TOWN"와 범주형 변수인 “CHAS” (Dummy variable)를 제외하여 모든 수치형 변수에 대해서 표준화를 진행합니다.

1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler

# feature standardization  (numerical_columns except dummy var.-"CHAS")
scaler = StandardScaler()  # 평균 0, 표준편차 1
scale_columns = ['CRIM', 'ZN', 'INDUS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT']
df[scale_columns] = scaler.fit_transform(df[scale_columns])
1
df.head()
TOWN LON LAT CMEDV CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 Nahant -70.955 42.2550 24.0 -0.419782 0.284830 -1.287909 0 -0.144217 0.413672 -0.120013 0.140214 -0.982843 -0.666608 -1.459000 0.441052 -1.075562
1 Swampscott -70.950 42.2875 21.6 -0.417339 -0.487722 -0.593381 0 -0.740262 0.194274 0.367166 0.557160 -0.867883 -0.987329 -0.303094 0.441052 -0.492439
2 Swampscott -70.936 42.2830 34.7 -0.417342 -0.487722 -0.593381 0 -0.740262 1.282714 -0.265812 0.557160 -0.867883 -0.987329 -0.303094 0.396427 -1.208727
3 Marblehead -70.928 42.2930 33.4 -0.416750 -0.487722 -1.306878 0 -0.835284 1.016303 -0.809889 1.077737 -0.752922 -1.106115 0.113032 0.416163 -1.361517
4 Marblehead -70.922 42.2980 36.2 -0.412482 -0.487722 -1.306878 0 -0.835284 1.228577 -0.511180 1.077737 -0.752922 -1.106115 0.113032 0.441052 -1.026501

>> Training set / Test set 나누기

나중에 도출될 예측 모델의 예측 성능을 평가하기 위해, 먼저 전체 데이터셋을 "Training set"과 "Test set"으로 나누겠습니다. Training set에서 모델을 학습하고 Test set에서 모델의 예측 성능을 검증할 겁니다.

1
2
# features for linear regression model
df[numerical_columns].head()
CRIM ZN INDUS CHAS NOX RM AGE DIS RAD TAX PTRATIO B LSTAT
0 -0.419782 0.284830 -1.287909 0 -0.144217 0.413672 -0.120013 0.140214 -0.982843 -0.666608 -1.459000 0.441052 -1.075562
1 -0.417339 -0.487722 -0.593381 0 -0.740262 0.194274 0.367166 0.557160 -0.867883 -0.987329 -0.303094 0.441052 -0.492439
2 -0.417342 -0.487722 -0.593381 0 -0.740262 1.282714 -0.265812 0.557160 -0.867883 -0.987329 -0.303094 0.396427 -1.208727
3 -0.416750 -0.487722 -1.306878 0 -0.835284 1.016303 -0.809889 1.077737 -0.752922 -1.106115 0.113032 0.416163 -1.361517
4 -0.412482 -0.487722 -1.306878 0 -0.835284 1.228577 -0.511180 1.077737 -0.752922 -1.106115 0.113032 0.441052 -1.026501 

1
2
3
4
5
6
from sklearn.model_selection import train_test_split

# split dataset into training & test
X = df[numerical_columns]
y = df['CMEDV']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
1
X_train.shape, y_train.shape
((404, 13), (404,))


1
X_test.shape, y_test.shape
((102, 13), (102,))

>> 다중공선성

회귀 분석에서 하나의 feature(예측 변수)가 다른 feature와의 상관 관계가 높으면(즉, 다중공선성이 존재하면), 회귀 분석 시 부정적인 영향을 미칠 수 있기 때문에, 모델링 하기 전에 먼저 다중공선성의 존재 여부를 확인해야합니다.

보통 다중공선성을 판단할 때 VIF값을 확인합니다. 일반적으로, VIF > 10인 feature들은 다른 변수와의 상관관계가 높아, 다중공선성이 존재하는 것으로 판단합니다.

1
2
3
4
5
6
from statsmodels.stats.outliers_influence import variance_inflation_factor

vif = pd.DataFrame()
vif['features'] = X_train.columns
vif["VIF Factor"] = [variance_inflation_factor(X_train.values, i) for i in range(X_train.shape[1])]
vif.round(1)
features VIF Factor
0 CRIM 1.7
1 ZN 2.5
2 INDUS 3.8
3 CHAS 1.1
4 NOX 4.4
5 RM 1.9
6 AGE 3.2
7 DIS 4.2
8 RAD 8.1
9 TAX 9.8
10 PTRATIO 1.9
11 B 1.4
12 LSTAT 3.0

VIF값을 확인해보면, 모든 변수의 VIF값이 다 10 이하입니다. 따라서 다중공선성 문제가 존재하지 않아 모든 feature을 활용하여 회귀 모델링을 진행하면 됩니다.


3-2. 회귀 모델링

먼저 Training set에서 선형 회귀 예측 모델을 학습합니다.
그 다음 도출된 모델을 Test set에 적용해 주택 가격(“CMEDV”)을 예측합니다. 이 결과는 다중에 실제 “CMEDV” 값과 비교하여 모델의 예측 성능을 평가하는 데 활용하게 됩니다.

1
2
3
4
5
6
7
8
from sklearn import linear_model

# fit regression model in training set
lr = linear_model.LinearRegression()
model = lr.fit(X_train, y_train)

# predict in test set
pred_test = lr.predict(X_test)

3-3. 모델 해석

>> coefficients 확인하기

먼저 각 feature의 회귀 계수를 확인해보겠습니다.

1
2
# print coef
print(lr.coef_)
[-0.9479409   1.39796831  0.14786968  2.13469673 -2.25995614  2.15879342
  0.12103297 -3.23121173  2.63662665 -1.95959865 -2.05639351  0.65670428
 -3.93702535]


1
2
3
# "feature - coefficients" DataFrame 만들기
coefs = pd.DataFrame(zip(df[numerical_columns].columns, lr.coef_), columns = ['feature', 'coefficients'])
coefs
feature coefficients
0 CRIM -0.947941
1 ZN 1.397968
2 INDUS 0.147870
3 CHAS 2.134697
4 NOX -2.259956
5 RM 2.158793
6 AGE 0.121033
7 DIS -3.231212
8 RAD 2.636627
9 TAX -1.959599
10 PTRATIO -2.056394
11 B 0.656704
12 LSTAT -3.937025 

1
2
3
# 크기 순서로 나열
coefs_new = coefs.reindex(coefs.coefficients.abs().sort_values(ascending=False).index)
coefs_new
feature coefficients
12 LSTAT -3.937025
7 DIS -3.231212
8 RAD 2.636627
4 NOX -2.259956
5 RM 2.158793
3 CHAS 2.134697
10 PTRATIO -2.056394
9 TAX -1.959599
1 ZN 1.397968
0 CRIM -0.947941
11 B 0.656704
2 INDUS 0.147870
6 AGE 0.121033 

1
2
3
4
5
6
7
8
9
10
11
## coefficients 시각화

# figure size
plt.figure(figsize = (8, 8))

# bar plot
plt.barh(coefs_new['feature'], coefs_new['coefficients'])
plt.title('"feature - coefficient" Graph')
plt.xlabel('coefficients')
plt.ylabel('features')
plt.show()

png


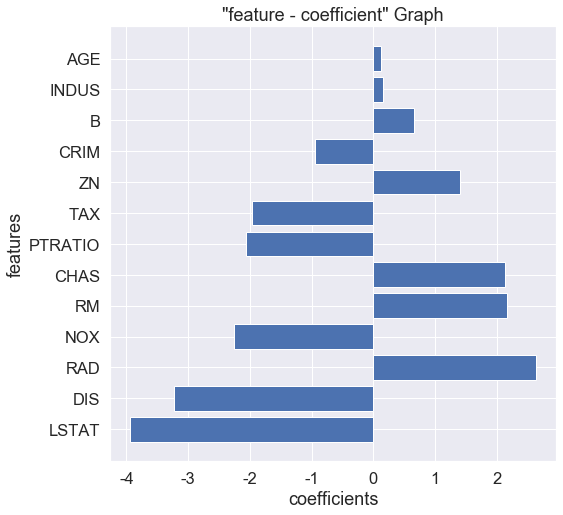
>> feature 유의성 검정

1
2
3
4
5
import statsmodels.api as sm

X_train2 = sm.add_constant(X_train)
model2 = sm.OLS(y_train, X_train2).fit()
model2.summary()
OLS Regression Results
Dep. Variable: CMEDV R-squared: 0.734
Model: OLS Adj. R-squared: 0.725
Method: Least Squares F-statistic: 82.86
Date: Tue, 11 Aug 2020 Prob (F-statistic): 1.72e-103
Time: 00:22:07 Log-Likelihood: -1191.9
No. Observations: 404 AIC: 2412.
Df Residuals: 390 BIC: 2468.
Df Model: 13
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
const 22.4313 0.245 91.399 0.000 21.949 22.914
CRIM -0.9479 0.290 -3.263 0.001 -1.519 -0.377
ZN 1.3980 0.372 3.758 0.000 0.667 2.129
INDUS 0.1479 0.458 0.323 0.747 -0.753 1.049
CHAS 2.1347 0.899 2.375 0.018 0.367 3.902
NOX -2.2600 0.490 -4.617 0.000 -3.222 -1.298
RM 2.1588 0.332 6.495 0.000 1.505 2.812
AGE 0.1210 0.415 0.292 0.771 -0.695 0.937
DIS -3.2312 0.477 -6.774 0.000 -4.169 -2.293
RAD 2.6366 0.671 3.931 0.000 1.318 3.955
TAX -1.9596 0.731 -2.679 0.008 -3.398 -0.522
PTRATIO -2.0564 0.319 -6.446 0.000 -2.684 -1.429
B 0.6567 0.272 2.414 0.016 0.122 1.191
LSTAT -3.9370 0.405 -9.723 0.000 -4.733 -3.141
Omnibus: 169.952 Durbin-Watson: 1.935
Prob(Omnibus): 0.000 Jarque-Bera (JB): 859.012
Skew: 1.762 Prob(JB): 2.94e-187
Kurtosis: 9.213 Cond. No. 10.7


Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

>> 주택 가격 영향 요소

위 결과를 종합해 보면, 주택 가격의 영향 요소에 관하여 다음과 같은 결론들을 도출할 수 있습니다:

  1. "INDUS"(상업적 비즈니스에 활용되지 않는 농지 면적)과 “AGE”(1940년 이전에 건설된 비율)은 유의하지 않습니다. (p value > 0.05)

  2. "ZN"(25,000 제곱 피트(sq.ft) 이상의 주택지 비율),
    "CHAS"(Charles 강과 접하고 있는지 여부),
    "RM"(자택당 평균 방 갯수),
    "RAD"(소속 도시가 Radial 고속도로와의 접근성 지수),
    "B"(흑인 지수)는
    주택 가격에 Positive한 영향을 미칩니다.
    즉, 다른 변수의 값이 고정했을 때, 해당 변수의 값이 클수록 주택의 가격이 높을 것입니다.

  3. "CRIM"(지역 범죄율),
    "NOX"(산화질소 농도),
    "DIS"(보스턴 고용 센터와의 거리),
    "TAX"(재산세),
    "PTRATIO"(학생-교사 비율),
    "LSTAT"(빈곤층 비율)은
    주택 가격에 Negative한 영향을 미칩니다.
    즉, 다른 변수의 값이 고정했을 때, 해당 변수의 값이 작을수록 주택의 가격이 높을 것입니다.


3-4. 모델 예측 결과 및 성능 평가

>> 예측 결과 시각화

학습한 모델을 Test set에 적용하여 y값(“CMEDV”)을 예측합니다.
예측 결과를 확인하기 위해 실제값과 예측값을 한 plot에 출력해 시각화해보겠습니다.

1
2
3
4
5
6
7
8
9
10
# 예측 결과 시각화 (test set)
df = pd.DataFrame({'actual': y_test, 'prediction': pred_test})
df = df.sort_values(by='actual').reset_index(drop=True)

plt.figure(figsize=(12, 9))
plt.scatter(df.index, df['prediction'], marker='x', color='r')
plt.scatter(df.index, df['actual'], alpha=0.7, marker='o', color='black')
plt.title("Prediction Result in Test Set", fontsize=20)
plt.legend(['prediction', 'actual'], fontsize=12)
plt.show()

png


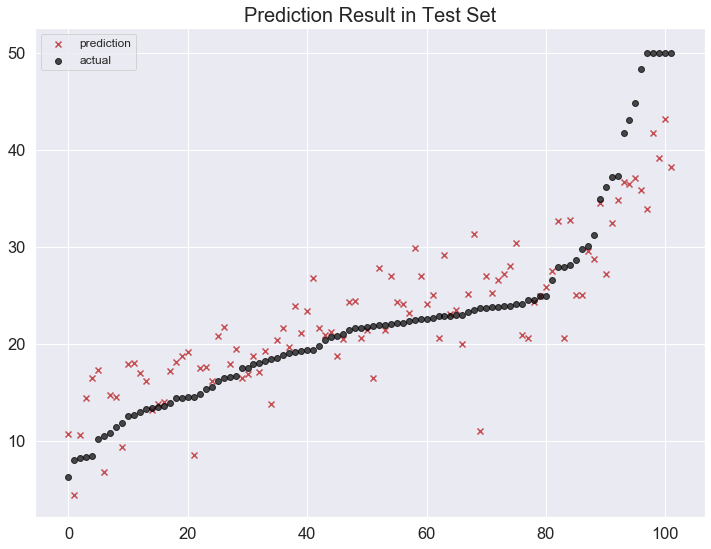
>> 모델 성능 평가

모델의 예측 성능을 평가하기 위해 모델의 R square과 RMSE를 계산해볼게요.

  • R square
1
2
3
# R square
print(model.score(X_train, y_train))  # training set
print(model.score(X_test, y_test))  # test set
0.7341832055169144
0.7639579157366423

  • RMSE
1
2
3
4
5
6
7
8
9
10
# RMSE
from sklearn.metrics import mean_squared_error
from math import sqrt

# training set
pred_train = lr.predict(X_train)
print(sqrt(mean_squared_error(y_train, pred_train)))

# test set
print(sqrt(mean_squared_error(y_test, pred_test)))
4.624051760840334
4.829847098176557

Test set에서 해당 예측 모델의 R square가 0.76이고, RMSE가 4.83입니다.